Bäume
BäumeBäume werden in vielen Bereichen der Informatik verwendet, da Suchen und Einfügen sehr effizient erfolgen können
| Operation | Erklärung | Aufwand | Schlimmster Fall |
|---|---|---|---|
| Einfügen/Löschen | Ändern des Baums | O(log(n)) | O(n) |
| Suchen | Suchen eines Elements | O(log(n)) | O(n) |
| Nächstes Element | Finden des nächsten Elements | O(1) | O(1) |
Da naiv implementierte Bäume degenerieren können und dann die Aufwände einer Liste haben, werden in der Vorlesung einige, wenige Optimierungen diskutiert. Diese Optimierung unterbinden den schlimmsten Fall eines Aufwands mit der Ordnung O(n).
Bäume sind hierarchische Datenstrukturen die aus einer verzweigten Datenstruktur bestehen. Bäume bestehen aus Knoten und deren Nachfolgern.
Jeder Knoten in einem Baum hat genau einen Vorgängerknoten. Der einzige Knoten für den das nicht gilt, ist der Wurzelknoten (engl. root) er hat keinen Vorgänger. Der Wurzelknoten stellt den obersten Knoten dar. Von dieser Wurzel aus kann man von Knoten zu Knoten zu jedem Element des Baums gelangen.
| Rekursive Definition eines Baums |
|---|
| Ein Baum besteht aus Unterbäumen und diese setzen sich bis zu den Blattknoten wieder aus Unterbäumen zusammen. |
Die Baumstruktur wird in Ebenen unterteilt.
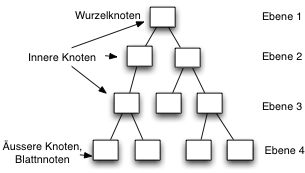
Die Tiefe eines Baumes ergibt sich aus der maximalen Anzahl der Ebenen.
Vollständige Bäume
| Vollständige Bäume |
|---|
| Ein Baum ist vollständig wenn alle Ebenen ausser der letzten Ebene vollständig mit Knoten gefüllt sind. |
Im folgenden Beispiel wird ein Baum gezeigt, der maximal drei Nachfolgerknoten pro Konten besitzen kann:
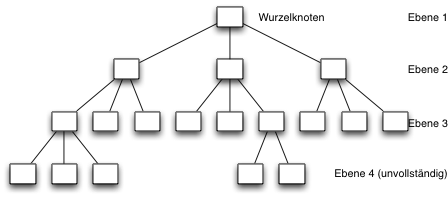
Binärbäume
Binärbäume bestehen aus Knoten mit maximal 2 Nachfolgerknoten. Die maximale Anzahl Knoten pro Ebene ist 2(k-1) Knoten in der Ebene k.
Streng sortierte Binärbäume
| Streng sortierte Binärbäume |
|---|
|
Für jeden Baumknoten gilt:
|
Beispiel eines streng sortierten Binärbaums:
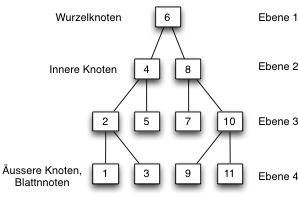
Suchen
Sortierte Binärbäume eignen sich sehr gut zum effektiven Suchen, da mit jedem Knoten die Auswahl der Kandidaten in der Regel halbiert wird.
Das Suchen in einem sortierten Baum geschieht nach dem folgenden, rekursiven Prinzip:
- Beginne mit dem Wurzelknoten
- Vergleiche den gesuchten Wert mit dem Wert des Knoten und beende die Suche wenn der Wert übereinstimmt.
- Suche im linken Teilbaum weiter wenn der gesuchte Wert kleiner als der aktuelle Knoten ist.
- Suche im rechten Teilbaum weiter wenn der gesuchte Wert größer als der Wert des aktuellen Knoten ist.
Bemerkung: Effektives Suchen ist nur in gutartigen (balancierten) Bäumen möglich. Gutartige Bäume haben möglichst wenig Ebenen. Schlechte Bäume zum Suchen sind degenerierte Bäume die im schlimmsten Fall pro Ebene nur einen Knoten besitzen. Solche degenerierten Bäume verhalten sich wie Listen.
Gutartige Bäume haben daher eine Tiefe T= ld(n+a) was auch dem Aufwand zum Suchen O (ld(n)) entspricht. Schlechte Bäume haben eine Tiefe T = n was zu einem Suchaufwand wie bei Listen, also O(n) führt.
Beispielprogramm
|
Das folgende Programm erlaubt es manuell einen Binärbaum aus Ganzzahlen aufzubauen. DownloadDas Programm steht als jar Datei zur Verfügung und kann nach dem Download wie folgt gestartet werden: java -jar BaumGUI.jar Es erlaubt das Einfügen und Entfernen von Blattknoten: |
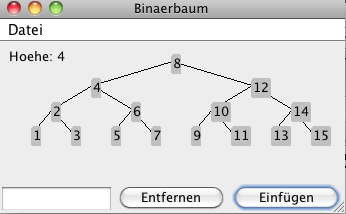 |
Alternative: Die Universität San Francisco hat eine sehr schöne webbasierte Visualisierung.
- 7886 views
AVL Bäume (Ausgeglichene Bäume)
AVL Bäume (Ausgeglichene Bäume)Binärbäume werden benutzt da sie ein sehr effizientes Suchen mit einem Aufwand von O(logN) erlauben solange sie balanciert sind. In extremen Fällen kann die Suche nach Knoten jedoch zu einem Aufwand von O(N) führen falls der Baum degeneriert ist.
Die im vorhergehenden Abschnitt vorgestellten Bäume verwenden in ihren Implementierungen der Einfüge- und Entferneoperation naive Verfahren. Diese naive Verfahren können dazu führen, dass ein Baum sehr unbalanciert werden kann.
Erste Vorschläge zur Vermeidung dieses Problems gehen auf die 1962 gemachten Vorschläge von Adelson-Velskij und Landis zurück. Sie schlugen höhenbalancierte AVL Bäume vor.
AVL Bäume
| AVL Baum |
|---|
|
Ein binärer Baum ist höhenbalanciert bzw AVL ausgeglichen wenn für jeden Knoten im Baum gilt:
|
Beispiele von AVL Bäumen die der obigen Definition genügen sind im folgenden Diagramm zu sehen
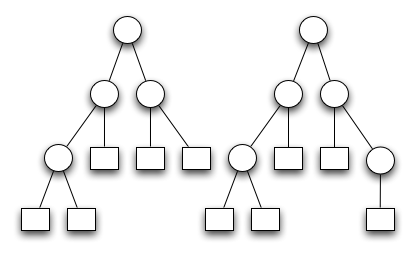
Der nachfolgende Baum ist kein AVL Baum. Der rechte Knoten in der zweiten Ebene von oben hat einen linken Unterbaum der Höhe 1 und einen rechten Unterbaum der Höhe 3.
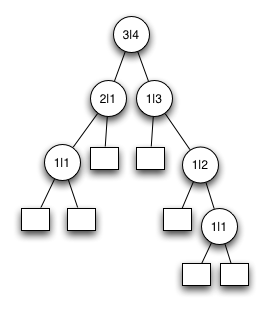
Dieser Baum müsste umorganisiert werden um ein AVL Baum zu werden.
Zum Verwalten von AVL Bäumen berechet man jedoch nicht immer wieder die Höhe der Teilbäume.
Es ist einfacher einen Balanchefaktor zu jedem inneren Knoten mitzuführen der die Differenz der Höhe vom linken und rechtem Teilbaum verwaltet.
| Balancefaktor bal(p) eines AVL Baums |
|---|
|
bal(p) = (Höhe rechter Teilbaum von p) - (Höhe linker Teilbaum von p) bal(p)∈{-1,0,1} |
Im folgenden Beispiel sind die Balancefaktoren für die inneren Knoten eingetragen:
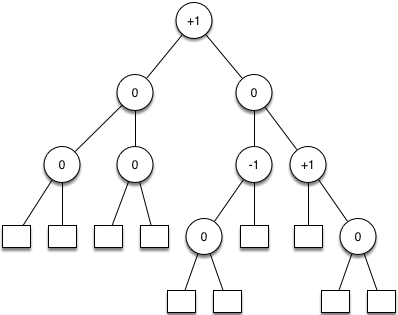
AVL Bäume müssen beim Einfügen und Entfernen von Knoten unter Umständen neu balanciert werden. Der Vorteil besteht jedoch in dem sehr vorhersagbaren Verhalten mit dem Aufwand von O(logN) bei Operationen auf dem Baum.
Tipp: Bauen Sie sich Ihren eigen AVL Baum. Die Universität hat eine web basierte Visualisierung von AVL Bäumen.
- 12034 views
Definition AVL-Baum, 2. Abb.
Kann es sein, dass bei den korrekten AVL-Bäumen unten rechts ein Kästchen fehlt? Dort ist bei einem Kreis lediglich ein Kästchen.
- Log in to post comments
Bruderbäume
BruderbäumeBruderbäume kann man als expandierte AVL Bäume verstehen.
Bruderbäume bekommen durch gezieltes Einfügen unärer Knoten eine konstante Tiefe für alle Blätter. Sie sind höhenbalancierte Bäume. Mit ihnen lässt sich garantieren, dass man mit dem gleichen Suchaufwand auf alle Blätter des Baums zugreifen kann.
Bruderbäume unterscheiden sich von den Binärbäumen dadurch, dass die inneren Knoten mindesten einen Sohn haben.
Bruderbäume haben ihren Namen von dem Fakt, dass für die Söhne eines Knoten untereinander (die Brüder) bestimmte Regeln gelten.
| Bruder |
|---|
| Zwei Knoten heißen Brüder wenn sie denselben Vater (Vorgängerknoten) haben. |
Ein binärer Baum ist ein Bruderbaum wenn das folgende gilt:
| Bruderbaum |
|---|
|
Ein Baum heißt Bruderbaum wenn die folgenden Bedingungen gelten:
|
Beispiele
Im folgenden Diagramm ist der rechte Baum ist kein Bruderbaum da es auf der zweiten Ebene von oben zwei unäre Bruder gibt.
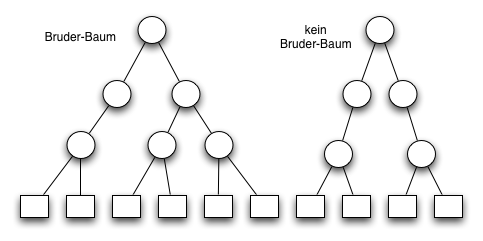
Im Diagramm unten ist der rechte Baum kein Bruderbaum weil die beiden Bruderknoten in der zweiten Ebene von oben unäre Brüder sind.
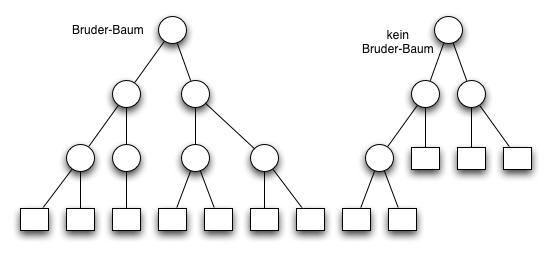
Bemerkung
Bei Bruderbäumen müssen bei Bedarf innerer Knoten eingefügt werden um die Bruderbedingungen zu erfüllen. Bruderbäume sind daher Bäume bei denen die zu verwaltenden Datenstrukturen nicht notwendigerweise in den inneren Knoten verwaltet werden können.
- 7786 views
Anzahl Söhne bei Bruderbäumen
Folgende, sich scheinbar widersprechende Aussagen entstammen Ihrem Skript. Was ist nun korrekt?
"Bruderbäume unterscheiden sich von den Binärbäumen dadurch, dass die inneren Knoten auch nur einen Sohn haben dürfen."
"Ein Baum heißt Bruderbaum wenn die folgenden Bedingungen gelten:
Jeder innere Knoten hat einen oder zwei Söhne."
- Log in to post comments
Gut beobachtet
Danke für den Kommentar.
Innere Knoten in Bruderbäumen müssen mindesten einen Sohn haben.
- Log in to post comments
Übungen (Bäume)
Übungen (Bäume)Balancierte und unbalancierte Bäume
Das folgende Programm erlaubt es manuell einen streng geordneten Binärbaum aus Ganzzahlen aufzubauen.
Das Programm steht als jar Datei zur Verfügung und kann nach dem Download wie folgt gestartet werden:
java -jar BaumGUI.jar
Balancierter Baum
Benutzen Sie das Beispielprogramm und erzeugen sie einen balancierten Baum mit 15 Knoten und der Höhe 4 wie zum Bsp.:

In welcher Reihenfolge müssen die Werte eingegeben werden?
Degenerierter Baum
Erzeugen Sie einen degenerierten Baum mit 5 Knoten und der Höhe 5:
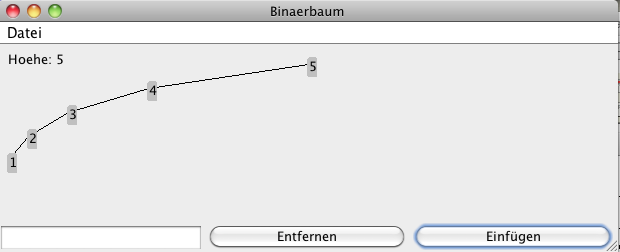
Welche Eingabefolgen von Zahlen erzeugen eine Liste degenerierten Teilbäumen?
Implementierung einer Binärbaums
Alle Klassen zu dieser Übung sind auch über github verfügbar.
Implementieren Sie einen streng geordneten Binärbaum in dem man ganze Zahlen Einfügen und Löschen kann.
Es ist nicht notwendig einen balancierten Baum oder AVL Baum zu implementieren.
Vervollständigen Sie die 3 drei fehlenden Methoden:
- s2.baum.Baumknoten
- Methode hoehe() : Implementieren Sie eine rekursive Methode zum bestimmen der Höhe des Baums (1.ter Schritt)
- s2.baum.Binaerbaum
- Methode einfuegen(teilBaum, Knoten) (2.ter Schritt)
- Tipps
- Betrachten Sie zuerst Sonderfälle (fehlen von Söhnen)
- Welchen Teilbaum müssen Sie modifizieren wenn der neue Knoten kleiner als die aktuelle Wurzel ist?
- Welchen Teilbaum müssen Sie modifizieren wenn der neue Knoten größer als die aktuelle Wurzel ist?
- Fügen Sie keinen Knoten mit einem Wert ein, der schon existiert!
- Tipps
- Methode loeschen(teilBaum, Knoten) (3.ter Schritt)
- Tipps
- Was müssen Sie tun wen der aktuelle Knoten gelöscht werden muss?
- Was müssen Sie tun wenn der zu löschende Knoten die Wurzel des gesamten Baums ist?
- Tipps
- Methode einfuegen(teilBaum, Knoten) (2.ter Schritt)
Übersetzen Sie alle Klassen. Starten Sie die Anwendung mit
$ java s2.baum.BaumGUI
Testen Sie die Anwendung mit der automatisierten Generierung mit dem Befehl
$ java s2.baum.BaumGUI magic
Hinweis: Die Implementierung des Algorithmus zum Entfernen von Knoten ist sehr viel aufwendiger da viele Randbedingungen geprüft werden müssen. Implementieren Sie zu Beginn nur das Einfügen von Knoten und Testen Sie zuerst das Einfügen. Die aktuelle Trivialimplementierung zum Entfernen erlaubt das Übersetzen und Ausführen der Anwendung ohne das Knoten entfernt werden.
UML Diagramm der beteiligten Klassen:
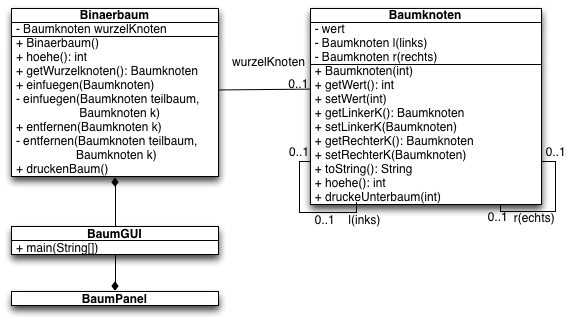
Notwendige Vorarbeiten
Erzeugen Sie die Infrastruktur für das folgenden Paket s2.baum
Klasse s2.baum.Baumknoten
package s2.baum;
/**
*
* @author s@scalingbits.com
*/
public class Baumknoten {
private int wert;
//private final int maxWert= Integer.MAX_VALUE;
private final int maxWert= 99;
public int getWert() {
return wert;
}
public void setWert(int wert) {
this.wert = wert;
}
/**
* Verwalte linken Knoten
*/
private Baumknoten l;
/**
* verwalte rechten Knoten
*/
private Baumknoten r;
public Baumknoten(int i) {wert=i;}
/**
* Liefere linken Knoten zurück
* @return linker Knoten
*/
public Baumknoten getLinkerK() {
return l;
}
/**
* Setze linken Knoten
* @param k Referenz auf linken Knoten
*/
public void setLinkerK(Baumknoten k) {
l = k;
}
/**
* Liefere rechten Knoten zurück
* @return rechter Knoten
*/
public Baumknoten getRechterK() {
return r;
}
/**
* Setze rechten Knoten
* @param k rechter Knoten
*/
public void setRechterK(Baumknoten k) {
r = k;
}
/**
* Drucken einen Unterbaum und rücke entsprechend bei Unterbäumen ein
* @param einruecken
*/
public void druckeUnterbaum(int einruecken) {
if (l != null) {
l.druckeUnterbaum(einruecken + 1);
}
for (int i = 0; i < einruecken; i++) {
System.out.print(".");
}
System.out.println(toString());
if (r != null) {
r.druckeUnterbaum(einruecken + 1);
}
}
/**
* Berechne Höhe des Baums durch rekursive Tiefensuche
* @return
*/
public int hoehe() {
System.out.println("Implementieren Sie Baumknoten.hoehe() als rekursive Methode");
return -1;
}
/**
* Generiere eine Zufallsbelegung für den gegebenen Knoten
* Die Funktion darf nicht mehr nach Einfügen in den Baum
* aufgerufen werden, da der neue Wert zu einer inkorrekten Ordnung führt
*/
public void generiereZufallswert() {
wert= (int)(Math.random()*(double)maxWert);
}
/**
* Erlaubt den Zahlenwert als Text auszudrucken
* @return
*/
public String toString() { return Integer.toString(wert);}
}
Klasse s2.baum.Binaerbaum
package s2.baum;
/**
*
* @author sschneid
*/
public class Binaerbaum {
private Baumknoten wurzelKnoten;
public Baumknoten getWurzelknoten() {return wurzelKnoten;}
/**
* Füge einen neuen Baumknoten in einen Baum ein
* @param s
*/
public void einfuegen(Baumknoten s) {
if (wurzelKnoten == null) {
// Der Baum ist leer. Füge Wurzelknoten ein.
wurzelKnoten = s;
}
else // Der Baum ist nicht leer. Normales Vorgehen
einfuegen(wurzelKnoten,s);
}
/**
* Füge einen gegebenen Knoten s in einen Teilbaum ein.
* Diese Methode ist eine rekursive private Methode
* Da der neue Knoten die Wurzel des neuen Teilbaums bilden kann,
* wird eventuell ein Zeiger auf einen neuen Teilbaum zurückgeliefert
* Randbedingung:
* * Es wird kein Knoten mit einem Wert eingefügt der schon existiertz
* @param teilbaum
* @param s
*/
private void einfuegen(Baumknoten teilbaum, Baumknoten s) {
System.out.println("Implementieren Sie die Methode Binaerbaum:einfuegen()");
}
/**
* Öffentliche Methoden zum Entfernen eines Baumknotens
* @param s
*/
public void entfernen(Baumknoten s) {
wurzelKnoten = entfernen(wurzelKnoten,s);}
/**
* Private, rekursive Methode zum Entfernen eines Knotens aus einem
* Teilbaum. Es kann ein neuer Teilbaum enstehen wennn der Wurzelknoten
* selbst entfernt werden muss. Der neue Teilbaum wird daher wieder mit
* ausgegeben
* @param teilbaum Teilbaum aus dem ein Knoten entfernt werden soll
* @param s der zu entfernende Knoten
* @return Der verbleibende Restbaum. Es kann auch Null für einen leeren Baum ausgegeben werden
*/
private Baumknoten entfernen(Baumknoten teilbaum, Baumknoten s) {
System.out.println("Implementieren Sie die Methode Binaerbaum:entfernen()");
return teilbaum;
}
/**
* Berechnung der Hoehe des Baums
* @return Hoehe des Baums
*/
public int hoehe() {
if (wurzelKnoten == null) return 0;
else return wurzelKnoten.hoehe();
}
/**
* Rückgabe des Namens
* @return
*/
public String algorithmus() {return "Binaerbaum";}
public void druckenBaum() {
System.out.println("Tiefe:" + hoehe());
if (wurzelKnoten != null) wurzelKnoten.druckeUnterbaum(0);
System.out.println("A-----------A");
}
}
Klasse s2.baum.BaumGUI
package s2.baum;
import java.awt.BorderLayout;
import java.awt.Container;
import java.awt.GridLayout;
import java.awt.event.ActionEvent;
import java.awt.event.ActionListener;
import javax.swing.JButton;
import javax.swing.JFrame;
import javax.swing.JLabel;
import javax.swing.JMenu;
import javax.swing.JMenuBar;
import javax.swing.JMenuItem;
import javax.swing.JPanel;
import javax.swing.JTextField;
/**
*
* @author s@scalingbits.com
*/
public class BaumGUI implements ActionListener {
final private JFrame hf;
final private JButton einfButton;
final private JButton entfButton;
final private JTextField eingabeText;
final private JMenuBar jmb;
final private JMenu jm;
final private JMenuItem exitItem;
final private BaumPanel myBaum;
final private Binaerbaum b;
public BaumGUI(Binaerbaum bb) {
b = bb;
JLabel logo;
//ButtonGroup buttonGroup1;
JPanel buttonPanel;
// Erzeugen einer neuen Instanz eines Swingfensters
hf = new JFrame("BaumGUI");
// Gewünschte Größe setzen
// 1. Parameter: horizontale Größe in Pixel
// 2. Parameter: vertikale Größe
hf.setSize(220, 230);
// Beenden bei Schliesen des Fenster
hf.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
// Erzeugen der Buttons und Texteingabefeld
eingabeText = new JTextField("17");
einfButton = new JButton();
einfButton.setText("Einfügen");
entfButton = new JButton();
entfButton.setText("Entfernen");
// Registriere die eigene Instanz
// zum Reagieren auf eine Aktion der beiden Buttons
einfButton.addActionListener(this);
entfButton.addActionListener(this);
// Einfügen der drei Komponenten in ein Panel
// Das Gridlayout führt zum Strecken der drei Komponenten
buttonPanel = new JPanel(new GridLayout(1, 1));
buttonPanel.add(eingabeText);
buttonPanel.add(entfButton);
buttonPanel.add(einfButton);
// Erzeugen des Panels zum Malen des Baums
myBaum = new BaumPanel(b);
// setze Titel des Frame
hf.setTitle(b.algorithmus());
// Erzeuge ein Menueeintrag zum Beenden des Programms
jmb = new JMenuBar();
jm = new JMenu("Datei");
exitItem = new JMenuItem("Beenden");
exitItem.addActionListener(this);
jm.add(exitItem);
jmb.add(jm);
hf.setJMenuBar(jmb);
Container myPane = hf.getContentPane();
myPane.add(myBaum, BorderLayout.CENTER);
myPane.add(buttonPanel, BorderLayout.SOUTH);
hf.pack();
hf.setVisible(true);
hf.setAlwaysOnTop(true);
}
/**
* Diese Methode wird bei allen Aktionen der Menüleiste oder
* der Buttons aufgerufen
* @param e
*/
public void actionPerformed(ActionEvent e) {
Object source = e.getSource();
int wert = 0;
try {
if (source == entfButton) { //Entfernen aufgerufen
wert = Integer.parseInt(eingabeText.getText());
b.entfernen(new Baumknoten(wert));
myBaum.fehlerText("");
myBaum.repaint();
eingabeText.setText("");
}
if (source == einfButton) { // Einfügen aufgerufen
wert = Integer.parseInt(eingabeText.getText());
b.einfuegen(new Baumknoten(wert));
myBaum.fehlerText("");
myBaum.repaint();
eingabeText.setText("");
}
if (source == exitItem) { // Beenden aufgerufen
System.exit(0);
}
} catch (java.lang.NumberFormatException ex) {
// Fehlerbehandlung bei fehlerhafter Eingabe
myBaum.fehlerText("Eingabe '" + eingabeText.getText() + "' ist keine Ganzzahl");
myBaum.repaint();
eingabeText.setText("");
}
}
public static void main(String[] args) {
BaumGUI sg = new BaumGUI(new Binaerbaum());
if ((args.length > 0) && (args[0].equalsIgnoreCase("magic"))) {
sg.magicMode(15);
}
}
public void magicMode(int anzahl) {
Baumknoten[] gz = new Baumknoten[anzahl];
for (int i = 0; i < gz.length; i++) {
gz[i] = new Baumknoten(0);
gz[i].generiereZufallswert();
}
try {
for (int i = gz.length - 1; i >= 0; i--) {
eingabeText.setText(gz[i].toString());
b.einfuegen(gz[i]);
Thread.sleep(800);
myBaum.repaint();
}
for (int i = 0; i < gz.length; i++) {
eingabeText.setText(gz[i].toString());
b.entfernen(gz[i]);
Thread.sleep(800);
myBaum.repaint();
}
} catch (InterruptedException e) {
}
}
}
Klasse s2.baum.BaumPanel
package s2.baum;
import java.awt.Color;
import java.awt.Dimension;
import java.awt.Graphics;
import javax.swing.JPanel;
/**
*
* @author s@scalingbits.com
*/
public class BaumPanel extends JPanel{
final private Binaerbaum b;
final private int ziffernBreite = 10 ; // Breite einer Ziffer in Pixel
final private int ziffernHoehe = 20; // Hoehe einer Ziffer in Pixel
private String fehlerString;
public BaumPanel(Binaerbaum derBaum) {
fehlerString = "";
b = derBaum;
setPreferredSize(new Dimension(600,200));
setDoubleBuffered(true);
}
/**
* Setzen des Fehlertexts des Fehlertexts
* @param s String mit Fehlertext
*/
public void fehlerText(String s) {fehlerString = s;}
/**
* Methode die das Panel überlädt mit der Implementierung
* der Baumgraphik
* @param g
*/
public void paintComponent(Graphics g) {
super.paintComponent(g);
int maxWidth = getWidth();
int maxHeight = getHeight();
Baumknoten k = b.getWurzelknoten();
if (k != null) { // Male Wurzelknoten falls existierend
g.setColor(Color.black);
g.drawString("Hoehe: " + b.hoehe(), 10, 20);
g.drawString(fehlerString, 10, 40);
paintKnoten(g,k,getWidth()/2, 20);
}
else {
g.setColor(Color.RED);
g.drawString("Der Baum ist leer. Bitte Wurzelknoten einfügen.",10,20);
}
}
/**
* Malen eines Knotens und seines Unterbaums
* @param g Graphicshandle
* @param k zu malender Knoten
* @param x X Koordinate des Knotens
* @param y Y Koordinate des Knotens
*/
public void paintKnoten(Graphics g,Baumknoten k, int x, int y) {
int xOffset = 1; // offset Box zu Text
int yOffset = 7; // offset Box zu Text
String wertString = k.toString(); // Wert als Text
int breite = wertString.length() * ziffernBreite;
int xNextNodeOffset = ((int)java.lang.Math.pow(2,k.hoehe()-1))*10;
int yNextNodeOffset = ziffernHoehe*6/5; // Vertikaler Offset zur naechsten Kn.ebene
if (k.getLinkerK() != null) {
// Male linken Unterbaum
g.setColor(Color.black); // Schriftfarbe
g.drawLine(x, y, x-xNextNodeOffset, y+yNextNodeOffset);
paintKnoten(g,k.getLinkerK(),x-xNextNodeOffset,y+yNextNodeOffset);
}
if (k.getRechterK() != null) {
// Male rechten Unterbaum
g.setColor(Color.black); // Schriftfarbe
g.drawLine(x, y, x+xNextNodeOffset, y+yNextNodeOffset);
paintKnoten(g,k.getRechterK(),x+xNextNodeOffset,y+yNextNodeOffset );
}
// Unterbäume sind gemalt. Male Knoten
g.setColor(Color.LIGHT_GRAY); // Farbe des Rechtecks im Hintergrund
g.fillRoundRect(x-xOffset, y-yOffset, breite, ziffernHoehe, 3, 3);
g.setColor(Color.black); // Schriftfarbe
g.drawString(wertString, x+xOffset, y+yOffset);
}
}
Baumschule...
Fragen zu Binärbäumen
Welche der beiden Bäume sind korrekte, streng sortierte Binärbäume?
Welche sind keine streng sortierten Binärbäume und warum?
Streng sortierter Binärbaum 1
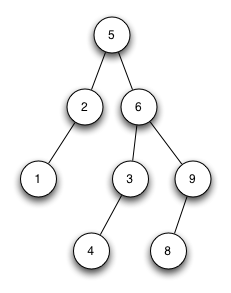
Streng sortierter Binärbaum 2
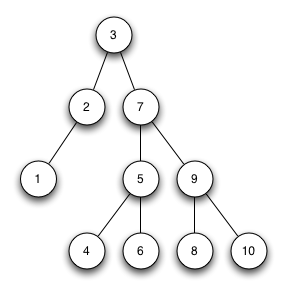
AVL Bäume
Welche der beiden AVL-Bäume sind korrekte AVL-Bäume?
Welche Bäume sind keine korrekten AVL Bäume und warum?
AVL-Baum 1
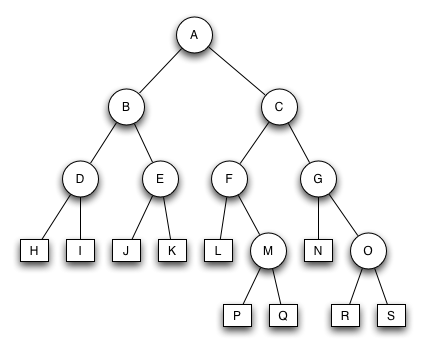
AVL Baum 2
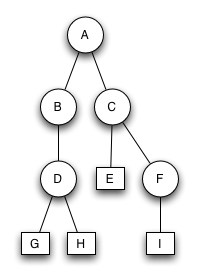
Bruder-Baum
Welche der beiden Bäume sind keine korrekten Bruder-Bäume?
Warum sind sie keine Bruderbäume?
Bruder-Baum 1
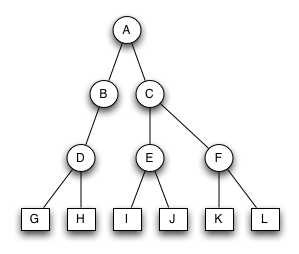
Bruder-Baum 2
Bruder-Baum 3
- 12860 views
Lösungen (Bäume)
Lösungen (Bäume)Balancierte und unbalancierte Bäume
Balancierter Baum
Eingabe: 8, 4, 12, 2, 6, 10, 14, 1, 3, 5, 7, 9, 11, 13, 15
Es sind auch andere Lösungen möglich.
Degenerierte Baum
Eingabemöglichkeiten
- 5, 4, 3, 2, 1
- 1, 2, 3, 4, 5
Sortierte Folgen, gleich ob sie fallend oder steigend sortiert sind, führen bei einfachen binären Bäumen zu degenerierten Bäumen mit großer Höhe.
Implementierung eines Binärbaums
Klasse s2.baum.Baumknoten
Informelle Beschreibung der Algorithmen
Höhe eines Baums
- Bestimme Höhe des linken Unterbaums
- Gibt es einen linkenUnterbaum?
- Nein: Höhe links =0
- Ja: Höhe links= Höhe linker Unterbaum
- Gibt es einen linkenUnterbaum?
- Bestimme Höhe des rechten Unterbaum
- Gibt es einen rechten Unterbaum?
- Nein: Höhe rechts = 0
- Ja: Höhe rechts = Höhe rechter Unterbaum
- Gibt es einen rechten Unterbaum?
- Bestimme den höchsten der beiden Unterbäume
- Höhe des Baumes= 1 + Höhe höchster Unterbaum
Quellcode
package s2.baum;
/**
*
* @author s@scalingbits.com
*/
public class Baumknoten {
private int wert;
//private final int maxWert= Integer.MAX_VALUE;
private final int maxWert= 99;
public int getWert() {
return wert;
}
public void setWert(int wert) {
this.wert = wert;
}
/**
* Verwalte linken Knoten
*/
private Baumknoten l;
/**
* verwalte rechten Knoten
*/
private Baumknoten r;
public Baumknoten(int i) {wert=i;}
/**
* Liefere linken Knoten zurück
* @return linker Knoten
*/
public Baumknoten getLinkerK() {
return l;
}
/**
* Setze linken Knoten
* @param k Referenz auf linken Knoten
*/
public void setLinkerK(Baumknoten k) {
l = k;
}
/**
* Liefere rechten Knoten zurück
* @return rechter Knoten
*/
public Baumknoten getRechterK() {
return r;
}
/**
* Setze rechten Knoten
* @param k rechter Knoten
*/
public void setRechterK(Baumknoten k) {
r = k;
}
/**
* Drucken einen Unterbaum und rücke entsprechend bei Unterbäumen ein
* @param einruecken
*/
public void druckeUnterbaum(int einruecken) {
if (l != null) {
l.druckeUnterbaum(einruecken + 1);
}
for (int i = 0; i < einruecken; i++) {
System.out.print(".");
}
System.out.println(toString());
if (r != null) {
r.druckeUnterbaum(einruecken + 1);
}
}
/**
* Berechne Höhe des Baums durch rekursive Tiefensuche
* @return
*/
public int hoehe() {
int lmax = 1;
int rmax = 1;
int max = 0;
if (l != null) lmax = 1 + l.hoehe();
if (r != null) rmax = 1 + r.hoehe();
if (rmax > lmax) return rmax;
else return lmax;
}
/**
* Generiere eine Zufallsbelegung für den gegebenen Knoten
* Die Funktion darf nicht mehr nach EInfügen in den Baum
* aufgerufen werden, da der neue Wert zu einer inkorrekten Ordnung führt
*/
public void generiereZufallswert() {
wert= (int)(Math.random()*(double)maxWert);
}
/**
* Erlaubt den Zahlenwert als Text auszudrucken
* @return
*/
public String toString() { return Integer.toString(wert);}
}Klasse s2.baum.Binaerbaum
Informelle Beschreibung der Algorithmen
Einfügen von Knoten
- Ist der Wert des neuen Knoten gleich der Wurzel meines Baums?
- Ja: Fertig. Es wird nichts eingefügt
- Nein:
- Ist der Wert kleiner als mein Wurzelknoten?
- Ja: Der neue Knoten muss links eingefügt werden
- Gibt es einen linken Knoten?
- Nein: Füge Knoten als linken Knoten ein
- Ja: Rufe Einfügemethode rejursiv auf...
- Gibt es einen linken Knoten?
- Nein: Der neue Knoten muss rechts eingefügt werden
- Gibt es einen rechten Knoten?
- Nein: Füge Knoten als rechten Knoten ein
- Ja: Rufe Einfügemethode rekursiv auf...
- Gibt es einen rechten Knoten?
- Ja: Der neue Knoten muss links eingefügt werden
- Ist der Wert kleiner als mein Wurzelknoten?
Quellcode
package s2.baum;
/**
*
* @author s@scalingbits.com
*/
public class BinaerbaumLoesung {
private Baumknoten wurzelKnoten;
public Baumknoten getWurzelknoten() {return wurzelKnoten;}
/**
* Füge einen neuen Baumknoten in einen Baum ein
* @param s
*/
public void einfuegen(Baumknoten s) {
if (wurzelKnoten == null) {
// Der Baum ist leer. Füge Wurzelknoten ein.
wurzelKnoten = s;
}
else // Der Baum ist nicht leer. Normales Vorgehen
einfuegen(wurzelKnoten,s);
}
/**
* Füge einen gegebenen Knoten s in einen Teilbaum ein.
* Diese Methode ist eine rekursive private Methode
* Da der neue Knoten die Wurzel des neuen Teilbaums bilden kann,
* wird eventuell ein Zeiger auf einen neuen Teilbaum zurückgeliefert
* Randbedingung:
* * Es wird kein Knoten mit einem Wert eingefügt der schon existiertz
* @param teilbaum
* @param s
*/
private void einfuegen(Baumknoten teilbaum, Baumknoten s) {
if (!(s.getWert()==teilbaum.getWert())) {
// Nicht einfuegen wenn Knoten den gleichen Wert hat
if (s.getWert()<teilbaum.getWert()) {
// Im linken Teilbaum einfuegen
if (teilbaum.getLinkerK() != null)
einfuegen(teilbaum.getLinkerK(),s);
else teilbaum.setLinkerK(s);
}
else // Im rechten Teilbaum einfuegen
if (teilbaum.getRechterK() != null)
einfuegen(teilbaum.getRechterK(),s);
else teilbaum.setRechterK(s);
}
}
/**
* Öffentliche Methoden zum Entfernen eines Baumknotens
* @param s
*/
public void entfernen(Baumknoten s) {
wurzelKnoten = entfernen(wurzelKnoten,s);}
/**
* Private, rekursive Methode zum Entfernen eines Knotens aus einem
* Teilbaum. Es kann ein neuer Teilbaum enstehen wennn der Wurzelknoten
* selbst entfernt werden muss. Der neue Teilbaum wird daher wieder mit
* ausgegeben
* @param teilbaum Teilbaum aus dem ein Knoten entfernt werden soll
* @param s der zu entfernende Knoten
* @return Der verbleibende Restbaum. Es kann auch Null für einen leeren Baum ausgegeben werden
*/
private Baumknoten entfernen(Baumknoten teilbaum, Baumknoten s) {
Baumknoten result = teilbaum;
if (teilbaum != null) {
if (teilbaum.getWert()==s.getWert()) {
// der aktuelle Knoten muss entfernt werden
Baumknoten altRechts = teilbaum.getRechterK();
Baumknoten altLinks = teilbaum.getLinkerK();
if (altRechts != null) {
result = altRechts;
if (altLinks != null) einfuegen(result, altLinks);
}
else
if (altLinks!=null) result = altLinks;
else result = null;
}
else if (teilbaum.getWert()<s.getWert()) {
Baumknoten k = teilbaum.getRechterK();
teilbaum.setRechterK(entfernen(k,s));
}
else {
Baumknoten k = teilbaum.getLinkerK();
teilbaum.setLinkerK(entfernen(k,s));
}
}
return result;
}
/**
* Berechnung der Hoehe des Baums
* @return Hoehe des Baums
*/
public int hoehe() {
if (wurzelKnoten == null) return 0;
else return wurzelKnoten.hoehe();
}
/**
* Rückgabe des Namens
* @return
*/
public String algorithmus() {return "Binaerbaum";}public void druckenBaum() {
System.out.println("Tiefe:" + hoehe());
if (wurzelKnoten != null) wurzelKnoten.druckeUnterbaum(0);
System.out.println("A-----------A");
}
}
Baumschule...
Fragen zu Binärbäumen
Welche der beiden Bäume sind korrekte, streng sortierte Binärbäume?
Welche sind keine streng sortierten Binärbäume und warum?
Streng sortierter Binärbaum 1
Der Baum ist kein streng sortierter Binärbaum. Knoten 3 müsste rechter Sohn von Knoten 2 sein. Knoten 4 müsste rechter Sohn von Knoten 3 sein.

Streng sortierter Binärbaum 2
Der Baum ist ein streng sortierter Binärbaum.

AVL Bäume
Welche der beiden AVL-Bäume sind korrekte AVL-Bäume?
Welche Bäume sind keine korrekten AVL Bäume und warum?
AVL-Baum 1
Der Baum ist ein AVL-Baum. Alle Blätter sind auf nur zwei unterschiedlichen Ebenen angeordnet.

AVL Baum 2
Der Baum ist kein AVL Baum. Das Fehlen eines zweiten Sohns von Knoten B führt zu einem Unterschied von zwei Ebenen im Baum.

Bruder-Baum
Welche der beiden Bäume sind keine korrekten Bruder-Bäume?
Warum sind sie keine Bruderbäume?
Bruder-Baum 1
Der Baum ist ein Bruder-Baum. Alle Blätter sind auf der untersten Ebene. Der einzige unäre Knoten B hat einen binären Bruderknoten.

Bruder-Baum 2
Der Baum ist kein Bruder-Baum. Der Blattknoten E ist nicht auf der untersten Ebene.

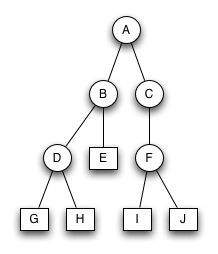
Bruder-Baum 3
Der Baum ist kein Bruder-Baum. Knoten B und C sind unäre Brüder. Einer von ihnen müsste binär sein.
Knoten B und C sind überflüssig. Nach ihrem Entfernen entsteht wieder ein Bruder-Baum.

- 11046 views