4. Prozedurales, modulares Programmieren, Unterprogramme, Funktionen, Methoden
4. Prozedurales, modulares Programmieren, Unterprogramme, Funktionen, Methoden Stefan Schneider Sat, 07/24/2010 - 17:30- 7665 views
4.1 Methoden
4.1 MethodenMethoden
Methoden sind ein wichtiges Strukturierungs- und Modularisierungsmittel.
Die Grundidee einer Methode ist wiederkehrende Aufgaben an einer Stelle zu implementieren und damit Redundanz zu vermeiden.
Ein zweiter wichtiger Aspekt ist die Senkung der Komplexität. Dem Benutzer muss die Implementierung einer Methode nicht bekannt sein um sie zu benutzen.
Der in Java verwendete Begriff wird in anderen Programmiersprachen auch wie folgt bezeichnet:
- Prozedur
- Unterprogramm
- Funktion
In Java wurden alle diese Begriffe der Übersichtlichkeit wegen im Begriff der Methode zusammen gefasst. Methoden gehören immer zu Klassen. Man kann in Java keine alleinstehenden Funktionen, Prozeduren etc. implementieren
Implementierung einer Methode
Methoden bestehen aus
- einem Methodenkopf bestehend aus der Deklaration
- Namen
- Signatur: Aufrufargumente, Rückgabewert
- Methodenrumpf
- der Rumpf wird von geschweiften Klammern eingeschlossen
- der Rumpf enthält die Implementierung der Methode
Zum Aufruf der Methode ist nur die Kenntnis der Deklaration notwendig

Methodenkopf
Durch ihn wird die Methode deklariert. Das bedeutet, das hiermit eine Schnittstelle festgelegt wird die alle Informationen enthält die ein Benutzer der Methode kennen muss um sie zu benutzen.
public static int multiplizieren( int faktor1, int faktor2) { // Methodenrumpf }
^ ^ ^ ^ ^
1. 2. 3. 4. 5.1. Zugriffsspezifikation; die Sichtbarkeit der Methode
- public : Die Methode darf von überall aufgerufen werden
- private: Die Methode darf nur innerhalb der Klasse verwendet werden
- protected: Die Methode darf nur innerhalb der Klasse oder von abgeleiteten Klassen verwendet werden
2. Statische Methoden: Das Schlüsselwort static erlaubt den Aufruf der Methode auch wenn es für die Klasse keine Instanz gibt. Das Konzept von Klassen, Objekten und Instanzen wird erst später eingeführt.
3. Rückgabetyp: Der Typ des Ergebnis welche die Methode zurückliefert. Es gibt zwei Möglichkeiten:
- Die Methode liefert ein Ergebnis zurück. Der Typ ist ein beliebiger Typ
- Die Methode liefert kein Ergebnis zurück. Hierzu wird das Schlüsselwort void verwendet.
4. Methodenname: Hiermit werden Methoden in einer Klasse unterschieden.
5. Parameterliste: Sie enthält den Typ und den Namen aller übergebenen Werte innerhalb von runden Klammern.
- Die übergebenen Werte werden in der Methode als Variablen verwendet.
- Die übergebenen Parameter werden mit Komma getrennt.
- Sollen einer Methode keine Parameter mitgegeben werden, so wird ein leeres Klammernpaar ohne Werte verwendet. Bsp. ()
- Die übergebenen Parametervariablen sind immer Kopien der aufrufenden Variablen. Dies bedeutet, dass man in der Methode eine Parametervariable ändern kann, ohne dass die Variable im äusseren Block die den Wert übergeben hat geändert wird.
Methodenrumpf
In Methodenrümpfe kann man:
- Variablen und Konstanten deklarieren
- Anweisungen und Schleifen ausführen
- Methoden der gleichen oder anderer Klassen aufrufen
- die Übergabeparameter nutzen
In Methoden können die im Methodenkopf deklarierten Parameter direkt verwendet werden. Bei einem gegebenen Rückgabeparameter muss dieser mit dem Schlüsselwort return zurückgegeben werden. Mit final bezeichnete Parameter dürfen im Methodenrumpf nicht mehr verändert werden. Beispiel
public static String textverkettung (String text, final int anzahl) {
String s="";
for (int i=0; i<anzahl; i++) {
s = s + text;
}
return s; }Die Rückgabe von Werten mit Hilfe des Schlüsselwort return funktioniert nicht nur mit Variablen, man kann auch Ausdrücke zurückgeben die den passenden Typ haben.
Wie zum Beispiel in der Methode textRahmen() die noch ein Textrahmen von jeweils 3 Zeichen um das Ergebnis legt:
public static String textRahmen (String text) {
return ">>>" + text + "<<<";
}Bei einem gegebenen Rückgabeparameter kann der Rumpf an verschiedenen Stellen verlassen werden.
Siehe Beispiel:
package s1.block4;
public class Textverkettung {
public static void main(String[] args) {
System.out.println(textverkettung("Sonnenschein", 3));
System.out.println(textverkettung("Sonnenschein", 0));
}
public static String textverkettung(String text, final int anzahl) {
String s="";
if (anzahl < 1) {
return "Gewählte Anzahl ist zu klein";
} else {
for (int i = 0; i < anzahl; i++) {
s = s + text;
}
return s;
}
}
}
Der Typ des Rückgabeparameter muss vom Typ her zum deklarierten Rückgabetyp der Methode passen.
Die Methode kann auch ohne einen Rückgabewert definiert werden. Im folgenden Beispiel wird sie den Text direkt selbst ausdrucken:
public class TextverkettungDrucken {
public static void main(String[] args) {
textverkettungDrucken("Sonnenschein", 3);
textverkettungDrucken("Sonnenschein", 0);
}
public static void textverkettungDrucken(String text, final int anzahl) {
String s="";
if (anzahl >0)
for (int i = 0; i < anzahl; i++)
s = s + text;
System.out.println("Ergebnis: " + s);
}
}
Aufruf von Methoden
Direkter Aufruf: Aufruf nur durch Methodenname und aktuelle Parameter
- Die aufgerufene Methode gehört zur gleichen Klasse oder einer Oberklasse (Fall 1 im Beispiel)
- Die Methode ist nicht statisch und wird auf das gleiche Objekt wie die umgebende Methode angewendet (Fall 1 im Beispiel)
- Die Methode ist statisch und kann ohne die Existenz eines Objekts verwendet werden (Fall 2 im Beispiel)
Aufruf mit vorgestelltem Objekt oder Klassenname (statische Methode)
- Die Methode soll für ein bestimmtes Objekt aufgerufen werden. Sie ist nicht statisch (Fall 3 im Beispiel)
- Die Methode ist statisch und gehört zu einer anderen Klasse. (Fall 4 im Beispiel)
Beispiel:
public class Flugzeug {
String kennzeichen;
int leerGewicht;
int besatzung;
public void drucken () {
System.out.println(kennzeichen + " , Crew: " + besatzung + ", "+leerGewicht + "kg");
}
public static void main(String[] args) {
Flugzeug f = new Flugzeug();
f.drucken();
f.kennzeichenAusgeben(); // Fall 3: Aufruf einer Methode für ein Objekt
eigenschaft(); // Fall 2: Aufruf einer statischen Methode der gleichen Klasse
Flughafen.eigenschaft(); // Fall 4: Aufruf einer statischen Methoden die zu einer anderen Klasse gehören kann
double pi = Math.sqrt(2.0); // Fall 4: Aufruf einer statischen Methoden die zu einer anderen Klasse gehört
}
public void kennzeichenAusgeben() {
drucken(); // Fall 1: Nicht statischer Methodenaufruf einer Methode der gleichen Klasse
}
public static void eigenschaft() {
System.out.println("kann fliegen");
}
}
public class Flughafen {
public static void eigenschaft() {
System.out.println("ist laut und schafft Arbeitsplätze");
}
}
Anwenden von Methoden
Methoden mit Eingabeparametern können bei jedem Aufruf mit anderen Werten arbeiten. Wichtig ist hierbei zu wissen, dass es bei mehreren Parameter auf die Reihenfolge der Parameter ankommt. Sie müssen beim Aufruf, in ihrer Reihenfolge, zur Deklaration passen. Der Übersetzer wird Parameter mit nicht passenden Typen als Fehler anzeigen. Sind die Typen mehrerer Parameter gleich oder kompatibel, muss der Entwickler selbst auf die Reihenfolge achten!
| Formalparameter von Methoden |
|---|
| Die in der Deklaration verwendeten Parameter einer Methode werden Formalparameter genannt |
| Aktualparameter von Methoden |
|---|
| Die beim Aufruf einer Methoden verwendeten Parameter werden Aktualparameter (aktuelle Parameter) genannt. |
Die oben gezeigte Methode textverkettung kann bei jedem Aufruf einen anderen Text verketten. Man kann die Methode wie folgt aufrufen.
package s1.block4;
public class Textverkettung {
public static void main(String[] args) {
String result;
String text1 = "Mustertext";
result= textverkettung("PingPong", 2);
System.out.println("Ergebnis: " + result);
result= textverkettung(text1, 3);
System.out.println("Ergebnis: " + result);
}
public static String textverkettung(String text, final int anzahl) {
String s;
s = text;
if (anzahl < 1) {
return "Gewählte Anzahl ist zu klein";
} else {
for (int i = 1; i < anzahl; i++) {
s = s + text;
}
return s;
}
}
}Das oben gezeigte Codestück sollte auf der Konsole das folgende Ergebnis ausdrucken:
Ergebnis: PingPongPingPong Ergebnis: MustertextMustertextMustertext
Der Aufruf von Methoden ohne Rückgabeparameter ist noch einfacher. Im folgenden Beispiel wird wie Methode textverketttungDrucken() aufgerufen:
...
String result;
String text1 = "Mustertext";
textverkettungDrucken("PingPong", 2); textverkettungDrucken(text1, 3);
...Man kann die Methode ohne eine Ergebnisvariable mit einer vereinfachten Syntax aufrufen. Ruft man Methoden mit Ergebnisvariablen in der oben gezeigten Form, ohne Zuweisung des Ergebnis zu einer Variablen, auf, so geht das Ergebnis verloren. Die Implementierung wird jedoch übersetzt und abgearbeitet. Es tritt keine Fehlermeldung auf.
Verschachtelte Methodenaufrufe und Methodenaufrufe innerhalb von Methoden
Methodenaufrufe mit Ergebnissen können überall benutzt werden wo in einem Ausdruck oder einer Zuweisung der entsprechende Typ gelesen werden soll.
Im folgenden Beispiel wird die Methode textverkettung() verschachtelt mit der Methode zur Rahmenerzeugung textRahmen() aufgerufen. Der geschachtelte Aufruf erfolgt in der Methode testTextRahmen():
public static String textverkettung(String text, final int anzahl) {
String s="";
if (anzahl < 1) {
return "Gewählte Anzahl ist zu klein";
} else {
for (int i = 0; i < anzahl; i++) {
s = s + text;
}
return s;
}
}
public static String textRahmen(String s) {
return "<< " + s + " >>";
}
public static void testTextRahmen() {
String s = "Inhalt";
String result = textRahmen(textverkettung(s,2));
System.out.println(result);
}
Ein Aufruf der Methode testTextRahmen() ergibt die Ausgabe:
<< InhaltInhalt >>
Methoden können nicht nur wie eben beschrieben geschachtelt werden. Man kann innerhalb eines Methodenrumpfes auch eine andere Methode aufrufen. Dies geschah oben in der Methode testTextRahmen.
Überladen von Methoden
Java erkennt eine Methode einer Klasse an den folgenden Merkmalen:
- Name der Methode
- Reihenfolge und Typ der Eingabeparameter
Man kann also den gleichen Namen einer Methode wiederverwenden solange sich die Typen der Eingabeparameter unterscheiden. Hiermit kann man Methoden implementieren, die "ähnliches" implementieren. Die "Ähnlichkeit" kann man mit dem gleichen Namen dokumentieren, die Parameterlisten müssen sich aber unterscheiden.
| Überladene Methoden |
|---|
| Überladene Methoden einer Klasse sind Methoden die den gleichen Namen besitzen und Formalparameterlisten mit unterscheidlichen Typen bzw. unterschiedlicher Anzahl von Parametern besitzen |
Überladene Methoden sind nützlich wenn man den prinzipiell gleichen Algorithmus für unterschiedliche Datentypen oder unterschiedliche Parameterkombinationen ausführen will.
Wichtig: Der Rückgabeparameter einer Methode wird in Java nicht bei der Unterscheidung überladener Methoden beachtet!
Methoden mit Rückgabeparameter können auch ohne Zuweisung ihres Rückgabewertes an eine Variable aufgerufen werden.
In diesem Fall kann der Übersetzer nicht feststellen welche Methode benutzt werden soll, wenn es mehrere Methoden gibt die sich nur im Rückgabewert unterscheiden.
Ein typisches Beispiel ist das drucken von unterschiedlichen Werten. Anbei vier überladene Methoden einer Klasse;
public class drucker {
public void drucken(String s) {
System.out.println("String:"+ s);
}
public void drucken(int i) {
System.out.println("Zahl: " + i);
}
public void drucken(String s, int i) {
System.out.println("String/Zahl" + s + "/" + i);
}
public void drucken(int i, String s) {
System.out.println("Anders: String/Zahl" + s + "/" + i);
}
}Die folgenden zwei Methoden sind keine erlaubten (zusätzlichen) überladene Methoden:
public void drucken(String z, int a) {
System.out.println("String/Zahl" + z + "/" + a);
}
public int drucken(String s, int i) {
System.out.println("String/Zahl" + s + "/" + i);
return 2*i;
}
Diese erste Methode besitzt die gleichen Formalparametertypen wie die dritte Methode. Die Namen der Parameter sind nicht relevant.
Die zweite Methode hat zwar einen anderen Rückgabeparameter, jedoch die gleichen Formalparameter wie die dritte Methode. Java ignoriert die Rückgabeparameter und verweigert das Übersetzen der Methode.
Entwurfsprinzipien für Methoden
- Methoden sollten eine klar definierte Teilaufgabe lösen
- Wird eine Methode groß und unübersichtlich sollte man sie in sinnvolle Teilmethoden zerlegen
- Gute Methoden werden an verschiedenen Stellen wieder verwendet
- Methoden sollten möglichst gekapselt sein
- Die Übergabeparameterlisten sollten so kurz wie möglich sein
- Methoden sollten möglichst wenig globale Variablen verwenden. Dem Verwender ist das nicht unbedingt bewusst!
- Ergebnisse sollten wenn möglich als Rückgabewert ausgegeben werden. Das Ändern von globalen Variablen sollte man wenn möglich vermeiden.
- Methoden und ihre Funktionen und Seiteneffekte sollten immer gut dokumentiert sein. Ein Verhältnis von Kommentar zu Quellcode von 1:1 ist durchaus vernünftig!
Programmstrukturierung mit Hilfe von Methoden
Methoden sind einer der Bausteine die die Entwicklung komplexer Anwendungen erlauben. Sie geben Strukturierungsmöglichkeiten um die Gesamtkomplexität von Anwendungen zu reduzieren:
- Abstraktion: Verwender einer Methode müssen nicht wissen wie sie intern funktioniert. Sie können sich auf die Beschreibung und die korrekte Ausführung der Methode verlassen
- Codereduktion: Das wieder verwenden von Methoden erlaubt es mit deutlich weniger Programmcode auszukommen. Die Kosten für die Pflege der Quellen und die Fehlerhäufigkeit der Anwendung sinkt. Bei replizierten Codestücken müssten alle Codestücke gefunden und individuell angepasst werden.
- Strukturierung und Hierarchisierung: Das explizite Zusammenfassen von Codestücken die eine bestimmte Aufgabe lösen erleichtert Verständnis und Pflege der Anwendung. Methoden erlauben durch Aufruf von anderen Methoden die Strukturierung in vielschichtige Hierarchien.
- Teile und Herrsche: Das abstrahieren und Verbergen der Implementierung (Information hiding) erlaubt die Zusammenarbeit in Teams und die Entwicklung komplexer Anwendungen. Das Konzept der Schnittstelle ist ein "Vertrag" zwischen Anbieter und Konsument bei dem nur die semantische Wirkung der Methode verstanden sein muss.
Methoden sind nur das erste von mehreren Strukurierungshilfsmittel der Sprache Java die im Rahmen dieser Vorlesung vorgestellt werden. Klassen, Pakete, Vererbung und globale vs. lokale Variablen sind andere Möglichkeiten.
- 10830 views
Überschrift
nur eine Kleinigkeit, aber das "Überladen von Methoden", das über dem Text "Java erkennt eine Methode einer Klasse an den folgenden Merkmalen:" in Konsolenausgabe steht, sollte sicher eigentlich als neue Überschrift gedacht sein, oder?
- Log in to post comments
Danke, stimmt!
Vielen Dank,
der Fehler wurde gerichtet und der dazugehörende Abschnitt etwas umformuliert.
- Log in to post comments
Ein kleiner Verbesserungsvorschlag
Eine Methode leitet doch einen Programmblock ein. Bei der Erklärung des Methodenkopfes endet dieser jedoch mit einem Semikolon. Vielleicht kann man diesem noch mit einer geschweiften Klammer austauschen.
- Log in to post comments
4.2 Variablen, (Sichtbarkeit lokal, global)
4.2 Variablen, (Sichtbarkeit lokal, global)Variablen sind immer nur in einem gewissen Umfang sichtbar. Sichtbar bedeutet hier benutzbar, gültig.
Die Sichbarkeit von Variablen hängt vom Kontext, dem Block ab in dem sie deklariert worden sind.
Blöcke können sein:
- Programmcode zwischen geschweiften Klammern
- Programmcode innerhalb einer Schleife, Ausführungsektionen (z.Bsp. if Bedingung)
- Bereich einer Methode
- Bereich einer Klasse
- Global
Es gibt hier abhängig von der Sichtbarkeit verschiedene Bereiche
- Blocklokale Variablen
- Methodenlokale Variablen
- Klassenlokale Variablen

Die Gültigkeit von Variablen steht im Zusammenhang mit dem Stapel (Stackkonzept) des Laufzeitsystems.
Das Laufzeitsystem legt beim Beginn eines jeden Blocks die neuen Variablen hinter den Variablen des gerade aktuellen Blocks an.
Nach dem Verlassen eines Blocks wird der Zeiger auf das obere Ende des Stapels wieder auf die Variablen des letzen Blocks zurückgesetzt.
Der Speicher der Variablen des verlassenen Blocks ist hierdurch zur Wiederverwendung wieder freigegeben worden.
Das Verfahren eines Stapels entspricht der üblichen Handhabung von Tellern im Schrank.
- Neue Teller (hier Blöcke) werden immer oben an den Stapel angefügt
- Nicht mehr benötigte Teller werden nur von oben entfernt
Das Stackkonzept des Laufzeitssystems:
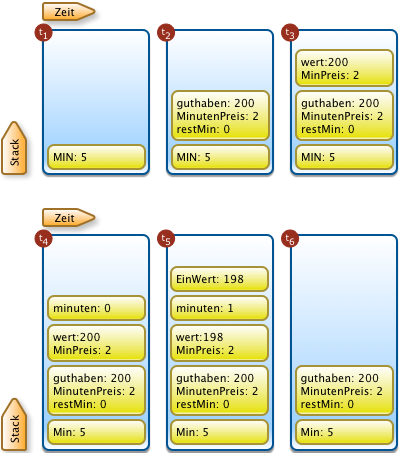
- 8527 views
public int guthaben
Hallo Hr. Schneider,
in der main-Methode steht public int guthaben = 200; im Stack steht guthaben mit einem Wert von 20.
Müsste der Wert im Stack nicht auch 200 haben?!
Viele Grüße
- Log in to post comments
4.3 Konstruktoren (1)
4.3 Konstruktoren (1)Konstruktoren sind spezielle Methoden mit denen Objekte einer Klasse initialisert werden. Das Java Laufzeitsystem legt automatisch einen Standardkonstruktor an wenn kein klassenspezifischer Konstruktor implementiert wird.
Konstruktoren haben die folgende Eigenschaften
- Der Konstruktor hat immer den Namen der Klasse als Methodenname
- Konstruktoren haben keine Rückgabewerte (auch kein Schlüsselwort void!)
- Die Auswahl des passenden Konstruktur erfolgt über die Typen der Eingabeparameter
- Konstruktoren können auch parameterlos sein
- Besitzt eine Klasse einen Konstruktor, so muss einer der Konstruktoren benutzt werden. Man kann die Klasse dann nicht mehr mit dem trivialen (System-)Konstruktor initialisieren.
Beispiel:
package s1.block4;
public class Employee {
public String surName;
public String firstName;
public int employeeId;
public double salary;
/**
* Der Konstruktor initialisert die Attribute für Employee
* @param ln Nachname
* @param fn Vorname
* @param id Mitarbeiternummer
* @param sal Gehalt. Gehalt wird im Konstruktor auf 100000 begrenzt
*/
public Employee (String ln, String fn, int id, double sal) {
surName = ln;
firstName = fn;
employeeId = id;
if (sal > 100000) salary = 100000;
else salary= sal;
}
public void printRecord() {
System.out.print(employeeId + ", " + surName + " " + firstName);
System.out.println(",Salary :" + salary);
}
/**
* Teste die Konstruktoren
* @param args werden nicht benutzt
*/
public static void main(String[] args) {
Employee ceo = new Employee("Doe","John",1,80000.0);
Employee cio = new Employee("Doe","Jane",1,70000.0);
ceo.printRecord();
cio.printRecord();
}
}
- 7832 views
4.4 Iteration und Rekursion
4.4 Iteration und RekursionIn den vorangegangen Abschnitten wurden verschiedene Schleifenkonstrukte vorgestellt mit denen man Codestrecken wiederholt durch laufen kann. Dieses Verfahren nennt man Iteration.
Methoden können aber nicht nur andere Methoden aufrufen, sie können auch sich selbst aufrufen. Dieses Verfahren nennt man Rekursion. Beide Verfahren sind von der Theorie her gleichwertig. Sie können wechselseitig eingesetzt werden. Im folgenden Beispiel wird die Multiplikation durch fortgesetzte Addition nach dem folgenden Prinzip iterativ und rekursiv gelöst.
Rekursive Algorithmen wenden das "Teile und Herrsche" Prinzip an indem Sie ein gegebenes Problem zerlegen in
- ein trivial lösbares Problem
- ein Restproblem welches gleich dem ursprünglichen Problem strukturiert ist (und einfacher ist!)
|
Die rekursive Methode fib() basiert auf den folgenden Definition von Fibonaccifolgen fib(0) = 0 (ein trivial lösbares Problem) fib(1) = 1 (ein trivial lösbares Problem) für alle n > 1 fib(n) = fib(n-1) + fib(n-2) (das einfachere Restproblem) |
Fibonacciberechnung |
Beispielprogramm:
package s1.block4;
public class Fibonacci {
public static long fib(int f) {
long ergebnis=0;
switch (f) {
case 0: { ergebnis = 0;break;} // Triviales Problem. Keine Rekursion
case 1: { ergebnis = 1;break;} // Triviales Problem. Keine Rekursion
default: { // Die Rekursion
ergebnis = fib(f - 1) + fib(f - 2);
break;
} // Ende default
} // Ende switch
return ergebnis;
} // Ende Methode
public static void main(String[] args) {
int a = 10; //Anzahl der berechneten Fibonaccizahlen
System.out.println("Fibonacciberechnung von fib(0) bis fib(" + a + ")");
for (int i=0; i<=a; i++)
System.out.println("fib("+i+")= " + fib(i));
} // Ende main()
} // Ende Klasse| Anmerkung: Diese naive Implementierung ist sehr ineffizient. Das Programm berechnet zu jeder Fibonaccizahl die beiden vorhergehenden Zahlen neu. Der Aufwand zur Berechnung der Fibonaccizahlen steigt daher exponentiell mit der Potenz 2. Dies macht den hier gewähltenAlhorithmus, zur Berechnung für größerer Fibonaccizahlen, ungeeignet. | 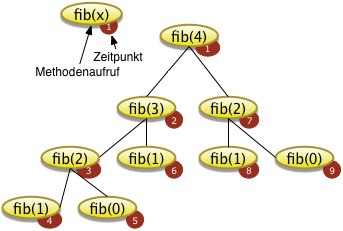 |
Beispiel: Quersummenberechnung
Die Methode berechne() berechnet eine Quersumme iterativ mit Hilfe einer while Schleife. Die Methode berechneRekursiv() berechnet das Ergebnis rekursiv (mit Selbstaufruf).
package s1.block4;
public class Quersumme {
/**
* Hauptprgramm zum Berechnen der Quersumme
* @param args wird nicht benutzt
*/
public static void main (String[] args) {
long eing = 12345678;
long ausg = berechne(eing);
System.out.println ("Ausgabe:" + ausg + "; Eing: " +eing);
System.out.println("Berechne rekursiv");
ausg = berechneRekursiv(eing);
System.out.println ("Ausgabe:" + ausg + "; Eing: " +eing);
}
/**
* Iterative Berechnung einer Quersumme mit einer while Schleife
* @param eing
* @return ausgabe
*/
public static long berechne(long eing){
long a = 0;
while (eing>0) { //Abbruch bei Null
a += eing%10; //Aufaddieren der letzen Stelle
eing /= 10; //Teilen der Zahl durch 10
}
return a;
}
/**
* Rekursive Berechnung einer Quersumme
* @param eing
* @return ausgabe
*/
public static long berechneRekursiv (long eing){
long a = 0;
if (eing>0) a = (eing%10)+berechneRekursiv(eing/10);
else a = 0; // Triviale Loesung. Nicht rekursiv.
return a;
}
}
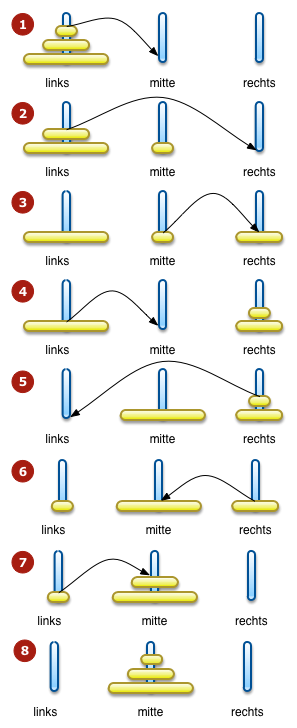
Beispiel: Die Türme von HanoiDie Türme von Hanoi sind ein einfaches Solitärspiel bei dem die folgenden Regeln gelten:
Siehe Wikipedia für weiterführende Erklärung und Animation. Die Strategie
|
Lösung für 3 Scheiben
|
Implementierung der Türme von Hanoi in Java
package s1.block4;
public class Hanoi {
public static void bewegeScheiben(int scheiben,
String von,
String nach,
String hilfsstab){
if (scheiben >0) {
bewegeScheiben(scheiben-1, von, hilfsstab,nach);
System.out.println(scheiben + ".te Scheibe von " + von + " nach " + nach );
bewegeScheiben(scheiben-1, hilfsstab, nach, von);
}
}
public static void main(String[] args) {
bewegeScheiben(3, "links", "mitte", "rechts");
}
}
Ablauf des Programmes
Konsolenausgabe1.te Scheibe von links nach mitte 2.te Scheibe von links nach rechts 1.te Scheibe von mitte nach rechts 3.te Scheibe von links nach mitte 1.te Scheibe von rechts nach links 2.te Scheibe von rechts nach mitte 1.te Scheibe von links nach mitte |
Rekursive Aufrufe der Methoden |
- 18546 views
4.5 Übungen
4.5 Übungen|
|
4.5.1 Übung: ArithmetikmethodenImplementieren Sie eine einfache Arithmetik für den Ganzzahltyp int sowie wie den Fließkommatyp double. Implementieren Sie für beide Typen die folgenden 4 Methoden:
Benutzen Sie die unten aufgeführte Klasse Main mit dem gegebenen Hauptprogramm um einige Tests auszuführen. |
Was geschieht wenn man die Operationen von verschiedenen Typen mischt?
package s1.block4;
public class Rechenarten {
/* Implementierung */
public static void main(String[] args) {
double ergebnis1;
int ergebnis2;
ergebnis1 = add(5.0, 4.0);
System.out.println(" 5.0 + 4.0 = " + ergebnis1);
ergebnis1 = div(9.0, 4.0);
System.out.println(" 9.0 / 4.0 = " + ergebnis1);
ergebnis1 = sub(9.0, 4.0);
System.out.println(" 9.0 - 4.0 = " + ergebnis1);
ergebnis1 = add(div(9.0, 4.0), 3.0);
System.out.println(" 9.0 / 4.0 + 3.0 = " + ergebnis1);
ergebnis2 = add(5, 4);
System.out.println(" 5 + 4 = " + add(5, 4));
ergebnis2 = div(9, 4);
System.out.println(" 9 / 4 = " + div(9, 4));
ergebnis2 = sub(9, 4);
System.out.println(" 9 - 4 = " + sub(9, 4));
ergebnis2 = add(div(9, 4), 3);
System.out.println(" 9 / 4 + 3 = " + add(div(9, 4), 3));
}
}4.5.2 Übung: Flächenberechnung von Dreiecken
Implementieren Sie eine Klasse mit Namen Dreieck. Die Klasse soll Methoden zu Flächenberechnung enthalten. Implementieren sie einzelne Methoden zur Berechnung der folgenden Dreieckstypen. Passen Sie die Anzahl der Parameter an die Gegebenheiten an
- beliebiges Dreieck: 3 Seiten gegeben
- gleichschenkliges Dreieck; 2 Seiten gegeben
- gleichseitiges Dreieck: 1 Seite gegeben
- rechtwinkliges Dreieck:
- 2 Katheten gegeben
- 1 Hypotenuse, 1 Kathete gegeben
Nutzen Sie wenn möglich schon implementierte Methoden zur Berechnung der Fläche. Dies bedeutet, dass man ein gleichschenkliges Dreieck für das man nur zwei Eingabeparameter benötigt mit Hilfe der Methode zur Berechnung eines allgemeinen Dreiecks berechnen kann. Das gleichschenklige Dreieck ist ein Spezialfall des allgemeinen Dreiecks.
Tipp:
- Nutzen Sie den Satz von Heron
- Benutzen Sie die Systemklasse Math für das Ziehen der benötigten Wurzel. Dies geschieht mit Math.sqrt().
- Hinweis. Durch das vorranstellen von Math. benötigen Sie keine Importdeklaration für das Math-Paket.
4.5.3 Übung: Rekursive Addition und Multiplikation
1. Übersetzen Sie das gegebene Beispielprogramm und testen Sie die Funktionsweise
- Vereinfachung: Die Anwendung muss nur für nicht negative Zahlen funktionieren
package s1.block4;
public class Arithmetik { /**
* Liest von der Kommazeile zwei Ganzzahlen ein und multipliziert sie
* @param args
*/
public static void main(String[] args) {
int a=5;
int b=8;
int c=0;
if (args.length > 1) {
try {
a = Integer.parseInt(args[0]);
b = Integer.parseInt(args[0]);
} catch (NumberFormatException e) {
System.err.println("Argument muss Ganzzahl sein");
System.exit(1);
}
}
// Kontrolle der Eingaben
System.out.println("Eingabe a: " + a +"; b: " +b);
c = a *b;
// Ergebnisprüfung
System.out.print("Ergebnis c: " + c);
if (c == a*b)
System.out.println(" (korrekt)");
else
System.out.println(" (falsch. Richtig ist " + (a*b)+")");
}
}
2. Benutzen einer for-Schleife mit Addition
Ersetzen Sie die Anweisung:
c = a*b;
durch eine for Schleife in der nur noch addiert wird
3. Einführen einer Methode mult()
Ersetzen Sie die Berechnung des Ergebnisses mit einer for-Schleife durch einen Methodenaufruf:
c = mult(a,b);
Implementieren Sie eine dazu passende Methode mult() die die Multplikation mit der for-Schleife durchführt
4. Eine rekursive Methode mult()
Ersetzen Sie die for-Schleife in der Methode mult() durch einen rekursiven Aufruf.
Tipps:
- Sie benötigen eine Bedingung für das Rekursionsende
- Definition des zu selbst zu lösenden Teilproblems
- Delegation des Restproblems durch rekursiven Aufrufs
5. Ersetzen der Addition durch eine rekursive Additionsmethode add() die nur die Inkrementfunktion benutzt
In gesamten Anwendung sollte jetzt kein * oder + Operator mehr vorkommen...
4.5.4 Fragen
Typische klausurrelevante Fragen:
- Aus welchen 2 Teilen besteht eine Methode?
- Aus welchen Teilen besteht ein Methodenkopf?
- Welches Schlüsselwort wird verwendet wenn kein Rückgabewert existiert?
- Wie sieht die Parameterliste des Methodenkopfes aus falls es keine Eingabeparameter gibt?
- Nenne ein Beispiel für eine überladene Methode.
4.5.5 Beispiel aus der Vorlesung
Diese Klassen liegen im Paket s1.airlineSolution.block4.
Klasse Flugzeug
package s1.airlineSolution.block4;
/**
*
* @author stsch
*/
public class Flugzeug {
final static double durchschnittsgewicht = 75;
String kennzeichen;
int passagiere;
private double maximalesGewicht;
double minimalGewicht;
Flugzeug(double minGewicht, double maxGewicht) {
System.out.println("Hallo, ich baue ein Flugzeug");
maximalesGewicht = maxGewicht;
// Kontrolle des Minimalgewichts
if ((minGewicht > 0) && (minGewicht <= maximalesGewicht)) {
minimalGewicht = minGewicht;
} else {
minimalGewicht = 5;
}
// Eine schwachsinnige Initialisierung
passagiere = 1;
}
public double maxG() {
return maximalesGewicht;
}
public void einsteigen() {
passagiere++;
}
public void einsteigen(int einsteiger) {
passagiere = passagiere + einsteiger;
}
double gewicht() {
double ergebnis;
ergebnis = minGewicht + passagiere * durchschnittsgewicht;
return ergebnis;
}
}
Klasse Flughafen
package s1.airlineSolution.block4;
/**
*
* @author stsch
*/
public class Flughafen {
String name;
Flugzeug gate1;
Flugzeug gate2;
Flugzeug gate3;
Flugzeug gate4;
Flugzeug gate5;
Flugzeug gate6;
public static void main(String[] args) {
Flughafen pb;
pb = new Flughafen();
pb.name = "Paderborn";
Flugzeug lh1 = new Flugzeug(222.0D,100000D);
lh1.kennzeichen = "D-A123";
lh1.passagiere = 23;
Flugzeug lh2 = new Flugzeug(3333.0D,100000D);
lh2.kennzeichen = "D-A456";
lh2.passagiere = 11;
pb.gate1 = lh1;
lh1.einsteigen();
lh1.einsteigen();
double meinGewicht = lh1.gewicht();
lh1.gewicht();
pb.gate2 = lh2;
lh2.einsteigen(88);
System.out.println("Mein Flughafen: " + pb.name);
System.out.println("Gate 1: " + pb.gate1.kennzeichen +
", Passagiere: " + pb.gate1.passagiere +
", akt. Gew.: " + pb.gate1.gewicht());
System.out.println("Gate 2: " + pb.gate2.kennzeichen +
", Passagiere: " + pb.gate2.passagiere);
if (pb.gate3 == null) {
System.out.println("Gate 3: leer");
} else {
System.out.println("Gate 3: " + pb.gate3.kennzeichen);
}
}
}
- 10896 views
Aufgabe 4.5.2 Rechtschreibfehler
In Aufgabe 4.5.2 müsste es "Kathete" und nicht "Kathede" heißen
- Log in to post comments
4.6 Lösungen
4.6 Lösungen4.6.1 Arithmetikmethoden
public class Rechenarten {
public static double add(double a, double b) {
return (a + b);
}
public static double sub(double a, double b) {
return (a - b);
}
public static double mul(double a, double b) {
return (a * b);
}
public static double div(double a, double b) {
return (a / b);
}
public static int add(int a, int b) {
return (a + b);
}
public static int sub(int a, int b) {
return (a - b);
}
public static int mul(int a, int b) {
return (a * b);
}
public static int div(int a, int b) {
return (a / b);
}
public static void main(String[] args) {
double ergebnis1;
int ergebnis2;
ergebnis1 = add(5.0, 4.0);
System.out.println(" 5.0 + 4.0 = " + ergebnis1);
ergebnis1 = div(9.0, 4.0);
System.out.println(" 9.0 / 4.0 = " + ergebnis1);
ergebnis1 = sub(9.0, 4.0);
System.out.println(" 9.0 - 4.0 = " + ergebnis1);
ergebnis1 = add(div(9.0, 4.0), 3.0);
System.out.println(" 9.0 / 4.0 + 3.0 = " + ergebnis1);
ergebnis2 = add(5, 4);
System.out.println(" 5 + 4 = " + add(5, 4));
ergebnis2 = div(9, 4);
System.out.println(" 9 / 4 = " + div(9, 4));
ergebnis2 = sub(9, 4);
System.out.println(" 9 - 4 = " + sub(9, 4));
ergebnis2 = add(div(9, 4), 3);
System.out.println(" 9 / 4 + 3 = " + add(div(9, 4), 3));
}
}4.6.2 Flächenberechnung vom Dreieck
public class Dreiecksflaeche {
/**
* Berechnung der Fläche eines Deiecks mit drei beliebigen Seiten.
* Es wird nicht geprüft ob die Seitenlängen ein korrektes Dreieck ergeben
* @param a Länge Seite 1
* @param b Länge Seite 2
* @param c Länge Seite 3
* @return Fläche des Dreiecks
*/
public static double flaeche(double a, double b, double c) {
double s = (a+b+c)/2;
return Math.sqrt(s*(s-a)*(s-b)*(s-c));
}
/**
* Berechnung der Fläche eines gleichschenkligen Deiecks.
* Es wird nicht geprüft ob die Seitenlängen ein korrektes Dreieck ergeben
* @param gleicherSchenkel die Länge der beiden gleichlangen Seiten
* @param basis Länge der Basis
* @return
*/
public static double flaeche(double gleicherSchenkel, double basis) {
return flaeche(gleicherSchenkel,gleicherSchenkel,basis);
}
/**
* Berechnung der Fläche eines gleichschenkligen Deiecks
* @param gleicheSeite Länge der Seite
* @return
*/
public static double flaeche(double gleicheSeite) {
return flaeche(gleicheSeite,gleicheSeite);
}
/**
* Berechnung der Fläche eines rechtwinkligen Dreiecks mit zwei Katheden
* @param k1 Länge erste Kathede
* @param k2 Länge zweite Kathede
* @return Fläche
*/
public static double flaecheKathedenDreieckeck(double k1, double k2){
return flaeche(Math.sqrt(k1*k1+k2*k2),k1,k2);
}
/**
* Berechnung der Fläche eines rechtwinkligen Dreiecks mit einer
* Hypotenuse und einer Kathede
* @param h Länge Hypothenuse
* @param k Länge Kathede
* @return Fläche
*/
public static double flaecheKathedeHypothenuseDreieck(double h, double k){
return flaecheKathedenDreieckeck(k,Math.sqrt(h*h-k*k));
}
/**
* Hauptprogrsam zum Testen
* @param args keine Eingabeparameter
*/
public static void main(String[] args) {
double aa = 3.0d;
System.out.println(flaeche(aa,4D,5D));
System.out.println(flaeche(5D,4D));
System.out.println(flaeche(3D));
System.out.println(flaecheKathedenDreieckeck(3D,4D));
System.out.println(flaecheKathedeHypothenuseDreieck(5D,4D));
}
}
4.6.3 Rekursive Addition und Multiplikation
Multiplikation mit Hilfe einer addierenden for-Schleife:
public class Arithmetik1 {
public static void main(String[] args) {
int a=5;
int b=8;
int c=0;
if (args.length > 1) {
try {
a = Integer.parseInt(args[0]);
b = Integer.parseInt(args[0]);
} catch (NumberFormatException e) {
System.err.println("Argument muss Ganzzahl sein");
System.exit(1);
}
}
System.out.println("Eingabe a: " + a +"; b: " +b);
for (int i=0; i<b; i++) {
c += a;
}
System.out.print("Ergebnis c: " + c);
if (c == a*b)
System.out.println(" (korrekt)");
else
System.out.println(" (falsch. Richtig ist " + (a*b)+")");
}
}
Delegation an eine Methode
public class Arithmetik2 {
public static void main(String[] args) {
int a=5;
int b=8;
int c=0;
if (args.length > 1) {
try {
a = Integer.parseInt(args[0]);
b = Integer.parseInt(args[0]);
} catch (NumberFormatException e) {
System.err.println("Argument muss Ganzzahl sein");
System.exit(1);
}
}
System.out.println("Eingabe a: " + a +"; b: " +b);
c = mult(a,b);
System.out.print("Ergebnis c: " + c);
if (c == a*b)
System.out.println(" (korrekt)");
else
System.out.println(" (falsch. Richtig ist " + (a*b)+")");
}
public static int mult(int x, int y) {
int ergebnis=0;
for (int i=0; i<x; i++) {
ergebnis += y;
}
return ergebnis;
}
}
Eine rekursive Multiplikation
public class Arithmetik3 {
public static void main(String[] args) {
int a=5;
int b=8;
int c=0;
if (args.length > 1) {
try {
a = Integer.parseInt(args[0]);
b = Integer.parseInt(args[0]);
} catch (NumberFormatException e) {
System.err.println("Argument muss Ganzzahl sein");
System.exit(1);
}
}
System.out.println("Eingabe a: " + a +"; b: " +b);
c = mult(a,b);
System.out.print("Ergebnis c: " + c);
if (c == a*b)
System.out.println(" (korrekt)");
else
System.out.println(" (falsch. Richtig ist " + (a*b)+")");
}
/**
* Diese Methode multipliziert zwei Zahlen rekursiv.
* Sie funktioniert nur für x Werte die nicht negativ sind!
* @param x darf nicht negativ sein
* @param y
* @return Ergebnis einer Multiplikation
*/
public static int mult(int x, int y) {
int ergebnis=0;
if (x==0)
ergebnis=0;
else
ergebnis=mult(y,(x-1))+y;
return ergebnis;
}
}
Multiplikation mit rekursiver Addition und Multiplikation
public class Arithmetik4 {
public static void main(String[] args) {
int a=5;
int b=8;
int c=0;
if (args.length > 1) {
try {
a = Integer.parseInt(args[0]);
b = Integer.parseInt(args[0]);
} catch (NumberFormatException e) {
System.err.println("Argument muss Ganzzahl sein");
System.exit(1);
}
}
System.out.println("Eingabe a: " + a +"; b: " +b);
c = mult(a,b);
System.out.print("Ergebnis c: " + c);
if (c == a*b)
System.out.println(" (korrekt)");
else
System.out.println(" (falsch. Richtig ist " + (a*b)+")");
}
/**
* Diese Methode multipliziert zwei Zahlen rekursiiv.
* Sie funktioniert nur für x Werte die nicht negativ sind!
* @param x darf nicht negativ sein
* @param y
* @return Ergebnis einer Multiplikation
*/
public static int mult(int x, int y) {
int ergebnis=0;
if (x==0)
ergebnis=0;
else
ergebnis=add(mult(y,(x-1)),y);
return ergebnis;
}
/**
* Diese Methode addiert zwei Zahlen rekursiv.
* Sie funktioniert nur für x Werte die nicht negativ sind!
* @param x darf nicht negativ sein
* @param y
* @return Ergebnis einer Multiplikation
*/
public static int add(int x, int y) {
int ergebnis=0;
if (y==0)
ergebnis=x;
else {
ergebnis=add(x,(y-1));
ergebnis++;
}
return ergebnis;
}
}
- 6276 views
4.7 Lernziele
4.7 Lernziele|
|
Am Ende dieses Blocks können Sie:
|
Lernzielkontrolle
Sie sind in der Lage die folgenden Fragen zu Methoden zu beantworten und die Übung 4.5.4 (Fragen) zu lösen.
Feedback

- 5276 views