Lösungen (Bäume)

Balancierte und unbalancierte Bäume

Balancierter Baum

Eingabe: 8, 4, 12, 2, 6, 10, 14, 1, 3, 5, 7, 9, 11, 13, 15

Es sind auch andere Lösungen möglich.

Degenerierte Baum

Eingabemöglichkeiten

  • 5, 4, 3, 2, 1
  • 1, 2, 3, 4, 5

Sortierte Folgen, gleich ob sie fallend oder steigend sortiert sind, führen bei einfachen binären Bäumen zu degenerierten Bäumen mit großer Höhe.

Implementierung eines Binärbaums

Klasse s2.baum.Baumknoten

Informelle Beschreibung der Algorithmen

Höhe eines Baums

  • Bestimme Höhe des linken Unterbaums
    • Gibt es einen linkenUnterbaum?
      • Nein: Höhe links =0
      • Ja: Höhe links= Höhe linker Unterbaum
  • Bestimme Höhe des rechten Unterbaum
    • Gibt es einen rechten Unterbaum?
      • Nein: Höhe rechts = 0
      • Ja: Höhe rechts = Höhe rechter Unterbaum
  • Bestimme den höchsten der beiden Unterbäume
  • Höhe des Baumes= 1 + Höhe höchster Unterbaum

Quellcode

 

package s2.baum;

/**
*
* @author s@scalingbits.com
*/
public class Baumknoten {
   private int wert;
   //private final int maxWert= Integer.MAX_VALUE;
   private final int maxWert= 99;
  public int getWert() {
   return wert;
   }
   public void setWert(int wert) {
     this.wert = wert;
   }
   /**
   * Verwalte linken Knoten
   */
   private Baumknoten l;
   /**
   * verwalte rechten Knoten
   */
   private Baumknoten r;
   public Baumknoten(int i) {wert=i;}
   /**
   * Liefere linken Knoten zurück
   * @return linker Knoten
   */
   public Baumknoten getLinkerK() {
      return l;
   }
   /**
   * Setze linken Knoten
   * @param k Referenz auf linken Knoten
   */
   public void setLinkerK(Baumknoten k) {
      l = k;
   }
   /**
   * Liefere rechten Knoten zurück
   * @return rechter Knoten
   */
   public Baumknoten getRechterK() {
      return r;
   }
   /**
   * Setze rechten Knoten
   * @param k rechter Knoten
   */
   public void setRechterK(Baumknoten k) {
      r = k;
   }
   /**
   * Drucken einen Unterbaum und rücke entsprechend bei Unterbäumen ein
   * @param einruecken
   */
   public void druckeUnterbaum(int einruecken) {
      if (l != null) {
      l.druckeUnterbaum(einruecken + 1);
   }
   for (int i = 0; i < einruecken; i++) {
      System.out.print(".");
   }
   System.out.println(toString());
   if (r != null) {
      r.druckeUnterbaum(einruecken + 1);
   }
   }
   /**
   * Berechne Höhe des Baums durch rekursive Tiefensuche
   * @return
   */
   public int hoehe() {
      int lmax = 1;
      int rmax = 1;
      int max = 0;
      if (l != null) lmax = 1 + l.hoehe();
      if (r != null) rmax = 1 + r.hoehe();
      if (rmax > lmax) return rmax;
      else return lmax;
   }
   /**
   * Generiere eine Zufallsbelegung für den gegebenen Knoten
   * Die Funktion darf nicht mehr nach EInfügen in den Baum
   * aufgerufen werden, da der neue Wert zu einer inkorrekten Ordnung führt
   */
   public void generiereZufallswert() {
      wert= (int)(Math.random()*(double)maxWert);
   }
   /**
   * Erlaubt den Zahlenwert als Text auszudrucken
   * @return
   */
   public String toString() { return Integer.toString(wert);}
}

Klasse s2.baum.Binaerbaum

Informelle Beschreibung der Algorithmen

Einfügen von Knoten

  • Ist der Wert des neuen Knoten gleich der Wurzel meines Baums?
    • Ja: Fertig. Es wird nichts eingefügt
    • Nein:
      • Ist der Wert kleiner als mein Wurzelknoten?
        • Ja: Der neue Knoten muss links eingefügt werden
          • Gibt es einen linken Knoten?
            • Nein: Füge Knoten als linken Knoten ein
            • Ja: Rufe Einfügemethode rejursiv auf...
        • Nein: Der neue Knoten muss rechts eingefügt werden
          • Gibt es einen rechten Knoten?
            • Nein: Füge Knoten als rechten Knoten ein
            • Ja: Rufe Einfügemethode rekursiv auf...

Quellcode

package s2.baum;
/**
 *
 * @author s@scalingbits.com
 */
public class BinaerbaumLoesung {
    private Baumknoten wurzelKnoten;
    public Baumknoten getWurzelknoten() {return wurzelKnoten;}
    /**
     * Füge einen neuen Baumknoten in einen Baum ein
     * @param s
     */
    public void einfuegen(Baumknoten s) {
        if (wurzelKnoten == null) {
            // Der Baum ist leer. Füge Wurzelknoten ein.
            wurzelKnoten = s;
        }
        else // Der Baum ist nicht leer. Normales Vorgehen
           einfuegen(wurzelKnoten,s);
    }
    /**
     * Füge einen gegebenen Knoten s in einen Teilbaum ein.
     * Diese Methode ist eine rekursive private Methode
     * Da der neue Knoten die Wurzel des neuen Teilbaums bilden kann,
     * wird eventuell ein Zeiger auf einen neuen Teilbaum zurückgeliefert
     * Randbedingung:
     * * Es wird kein Knoten mit einem Wert eingefügt der schon existiertz
     * @param teilbaum
     * @param s
     */
    private void einfuegen(Baumknoten teilbaum, Baumknoten s) {
        if (!(s.getWert()==teilbaum.getWert())) {
            // Nicht einfuegen wenn Knoten den gleichen Wert hat
            if (s.getWert()<teilbaum.getWert()) {
                // Im linken Teilbaum einfuegen
                if (teilbaum.getLinkerK() != null)
                        einfuegen(teilbaum.getLinkerK(),s);
                else teilbaum.setLinkerK(s);
             }
            else // Im rechten Teilbaum einfuegen
                if (teilbaum.getRechterK() != null)
                        einfuegen(teilbaum.getRechterK(),s);
                else teilbaum.setRechterK(s);
        }
    }
    /**
     * Öffentliche Methoden zum Entfernen eines Baumknotens
     * @param s
     */
    public void entfernen(Baumknoten s) {
        wurzelKnoten = entfernen(wurzelKnoten,s);}
    /**
     * Private, rekursive Methode zum Entfernen eines Knotens aus einem
     * Teilbaum. Es kann ein neuer Teilbaum enstehen wennn der Wurzelknoten
     * selbst entfernt werden muss. Der neue Teilbaum wird daher wieder mit
     * ausgegeben
     * @param teilbaum Teilbaum aus dem ein Knoten entfernt werden soll
     * @param s der zu entfernende Knoten
     * @return Der verbleibende Restbaum. Es kann auch Null für einen leeren Baum ausgegeben werden
     */
    private Baumknoten entfernen(Baumknoten teilbaum, Baumknoten s) {
       Baumknoten result = teilbaum;
       if (teilbaum != null) {
         if (teilbaum.getWert()==s.getWert()) {
             // der aktuelle Knoten muss entfernt werden
            Baumknoten altRechts = teilbaum.getRechterK();
            Baumknoten altLinks = teilbaum.getLinkerK();
            if (altRechts != null) {
                result = altRechts;
                if (altLinks != null) einfuegen(result, altLinks);
            }
            else
                if (altLinks!=null) result = altLinks;
                else result = null;
         }
         else if (teilbaum.getWert()<s.getWert()) {
            Baumknoten k = teilbaum.getRechterK();
            teilbaum.setRechterK(entfernen(k,s));
            }
         else {
            Baumknoten k = teilbaum.getLinkerK();
            teilbaum.setLinkerK(entfernen(k,s));
            }
        }
        return result;
        }
    /**
     * Berechnung der Hoehe des Baums
     * @return Hoehe des Baums
     */
    public int hoehe() {
        if (wurzelKnoten == null) return 0;
        else                      return wurzelKnoten.hoehe();
    }
    /**
     * Rückgabe des Namens
     * @return
     */
    public String algorithmus() {return "Binaerbaum";}

public void druckenBaum() {
System.out.println("Tiefe:" + hoehe());
if (wurzelKnoten != null) wurzelKnoten.druckeUnterbaum(0);
System.out.println("A-----------A");
}
}

Baumschule...

Fragen zu Binärbäumen

Welche der beiden Bäume sind korrekte, streng sortierte Binärbäume?

Welche sind keine streng sortierten Binärbäume und warum?

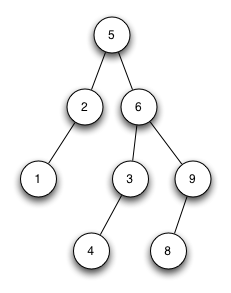
Streng sortierter Binärbaum 1

Der Baum ist kein streng sortierter Binärbaum. Knoten 3 müsste rechter Sohn von Knoten 2 sein. Knoten 4 müsste rechter Sohn von Knoten 3 sein.

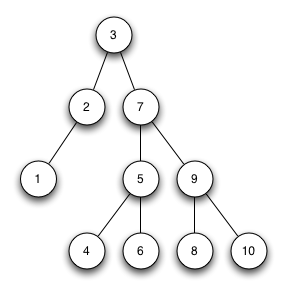
Streng sortierter Binärbaum 2

Der Baum ist ein streng sortierter Binärbaum.

AVL Bäume

Welche der beiden AVL-Bäume sind korrekte AVL-Bäume?

Welche Bäume sind keine korrekten AVL Bäume und warum?

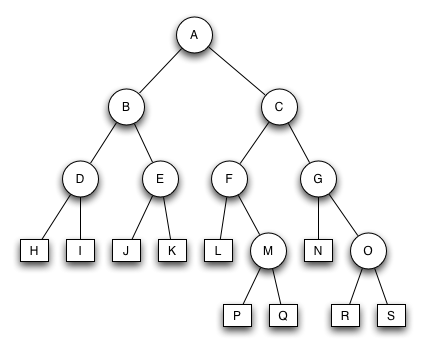
AVL-Baum 1

Der Baum ist ein AVL-Baum. Alle Blätter sind auf nur zwei unterschiedlichen Ebenen angeordnet.

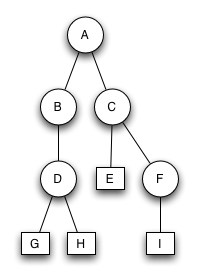
AVL Baum 2

Der Baum ist kein AVL Baum. Das Fehlen eines zweiten Sohns von Knoten B führt zu einem Unterschied von zwei Ebenen im Baum.

Bruder-Baum

 Welche der beiden Bäume sind keine korrekten Bruder-Bäume?

Warum sind sie keine Bruderbäume?

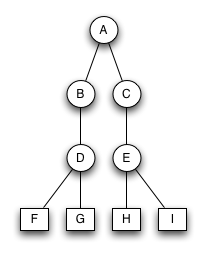
Bruder-Baum 1

Der Baum ist ein Bruder-Baum. Alle Blätter sind auf der untersten Ebene. Der einzige unäre Knoten B hat einen binären Bruderknoten.

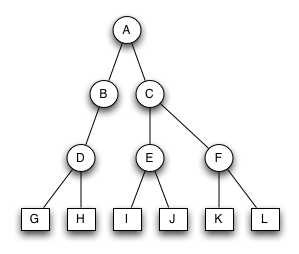
Bruder-Baum 2

Der Baum ist kein Bruder-Baum. Der Blattknoten E ist nicht auf der untersten Ebene.

 

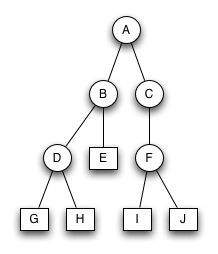
Bruder-Baum 3

Der Baum ist kein Bruder-Baum. Knoten B und C sind unäre Brüder. Einer von ihnen müsste binär sein.

Knoten B und C sind überflüssig. Nach ihrem Entfernen entsteht wieder ein Bruder-Baum.