|
|
7.4.1 Telefonbuchanwendung (1)Implementieren Sie eine Telefonbuchanwendung die es erlaubt die folgenden Datensätze zu verwalten:
|
Benötigte Zeit: 30-60 Minuten für einen gübten Programmierer
Die Klasse Telefonbuch soll die folgenden Eigenschaften haben:
- Verwaltung des Namens, Vornamens, Telefonnummer in drei Feldern mit den entsprechenden Typen
- Eine Methode die das gesamte Telefonbuch ausdruckt
- Suche nach allen drei Attributen mit drei verschiedenen Methoden
- Eine Methode zum "bevölkern" des Telefonbuchs mit mindestens 10 Namen
- Alle Datensätze seien unterschiedlich
- Das Telefonbuch soll initial Felder für 4 Einträge besitzen. Beim Vollaufen des Telefonbuchs sollen neue Felder angelegt werden die um 50% größer sind.
- Kapseln Sie die gesamte Implementierung der Felder innerhalb der Klasse
- Implementieren Sie eine Methode zum Löschen eines gesuchten Datensatzes
- Beim Löschen sollen keine leeren Einträge in den Feldern entstehen
- Implementieren Sie eine Testmethode die
- 10 Adressen einträgt
- 2 Adressen löscht
- 1 Adresse hinzufügt
Hinweise:
- Benutzen Sie Methoden für alle sinnvollen Teilaufgaben
- Das Telefonbuch ist nicht notwendigerweise sortiert. Man muss alle Datensätze durchsuchen
Tipp: Die Suchanfragen lassen sich mit wenig Aufwand vom einer grafischen Swingoberfläche steuern. Ein Beispielprogramm finden Sie hier.
7.4.2 "Objektorientierte" Telefonbuchanwendung (2)
Überarbeiten Sie die Telefonbuchanwendung aus der vorhergehenden Aufgabe derart, dass Sie:
- Eine Klasse Person mit den drei Attributen nutzen
- Nur ein Feld vom Typ Person in dem alle Daten verwaltet werden
Welche der beiden Lösungen gefällt Ihnen besser? Warum?
7.4.3 Zufallszahlengenerator
Schreiben Sie ein Programm welches die Zuverlässigkeit des Java Zufallszahlengenerator prüft.
- Erzeugen Sie ein Feld mit 1 Million (Anzahl konfigurierbar) Zufallszahlen im Bereich von 0 bis 999. Nutzen Sie die Methode Math.random() und das existierende Beispielprogramm.
- Erzeugen Sie ein dreidimensionales Feld für Ganzzahlen mit einer Größe von 10*10*10 Einträgen (Index jeweils 0..9).
- Speichern Sie in diesem Feld die Häufigkeit einer vorgekommenen Zahl.
- Bsp: Erhöhen sie den Zähler der Position [5][4][3] um wenn Sie eine Zufallszahl "534" gefunden haben. Die Zelle [5][4][3] speichert die Anzahl der gefundenen Zahlen "542".
- Zählen Sie die Zufallszahlen und tragen Sie sie in das dreidimensionale Feld ein
- Beispiel: Inkrementieren den Wert der Zelle array[2][4][5] für jedes Vorhandensein der Zahl 245
- Schreiben Sie eine Methode zum Ausdrucken des Feldes
- Schreiben Sie Methoden die die folgenden Fragen beantworten
- Welche Zahl kommen am häufigsten vor?
- Welche Zahl kommen am seltensten vor?
- Optional (keine Musterlösung):
- Gibt es lokale Häufungen?
- Welche Einer-, Zehner, Hunderterziffer ist am häufigsten?
- Haben Zellen mit über/unterdurchschnittlich vielen Einträgen auch Nachbarn mit über/unterdurchschnittlich vielen Einträgen?
- Eine Zelle array[x][y][z] hat meistens 8 Nachbarn array[x+/-1][y+/-1][z+/-1]
- Gibt es lokale Häufungen?
7.4.4 Conway: Das Spiel des Lebens
Das "Spiel des Lebens" wurde 1970 vom Mathematiker John Horton Conway 1970 entworfen.
Das Simulationsspiel basiert auf auf einem zweidimensionalen zellulären Automaten. Die Regeln des Automaten sind im Wikipediaartikel zu finden.
Die gelöste Aufgabe kann man in der unten genannten Anwendung sehen.
- Das Setzen von Elementen ist mit Mausklicks auf der entsprechenden Zelle möglich
- Eine neue Generation wird mit dem Button ">" berechnet
- Der Button ">>>" erlaubt das automatische Erzeugen von neuen Generationen. Mehrfaches Klicken halbiert die Wartezeit zwischen Generationen.
- Der Button "Stop" beendet den automatischen Modus
Laden Sie das jar-Archiv Conway.jar und starten Sie es im gleichen Verzeichnis mit dem Kommando
java -jar Conway.jar

Aufgabe
Vervollständigen die Klasse Generation.java. Nutzen Sie das Hauptprogramm SpielDesLebens.java zum Testen Ihrer Klasse.
Die Interaktion der Klasse Generation mit dem Rahmenprogramm ist im folgenden Diagramm dargestellt:
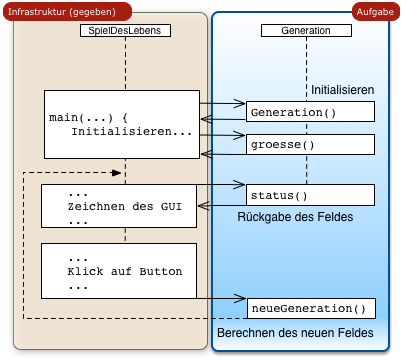
Klasse Generation.java
Hinweise:
- Das Hauptprogramm erwartet die Klasse Generation mit den vorgegebenen Methoden im gleichen Paket
- Sie können weitere Methoden wenn nötig implementieren
- Das Hauptprogramm wird genau eine Instanz der Klasse Generation erzeugen.
Beim Berechnen der Nachbarn eines Feldes ist auf die Sonderfälle am Rand zu achten:
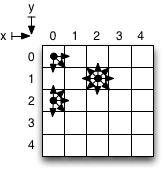
Weitere Hilfestellungen sind den Kommentaren zu entnehmen. Die Klasse kann natürlich auch ohne die Hilfestellung entwickelt werden. Das Feld kann initial zum Testen sehr klein (2) sein. Die Buttons werden dann erst nach dem Vergrößern des Fenster sichtbar. Eine Größe von 50x50 ist für aktuelle Rechner ausführbar. Pro Zelle werden etwa 10 Pixel benötigt.
package s1.block7;
/*
* @author scalingbits.com
*/
public class Generation {
// Hier ein Feld für alten Zustand deklarieren
// Hier ein Feld für neuen Zustand deklarieren
// die Felder muessen zweidimensional, vom Typ boolean sein, quadratisch sein/**
* Groesse des quadratischen Feldes
*/
// Variable für Groesse des Feldes anlegen. Empfohlen 50 ==> GUI benötigt dann etwa 500 Pixel
/**
* Anlegen aller benoetigten Felder mit Initialwerten
* Alle Feldelemente sollen mit dem Zustand "false" = leer versehen sein
*/
public Generation() {
// Initialisieren sie die beiden Felder
// alle Felder sollen den Zustand "false" haben. Dies ist ein leeres Feld
}
/**
*
* @return Kantenlaenge des quadratischen Felds
*/
public int groesse() {return 0;} //Richtigen Wert zurueckgeben!!
/**
* Berechnen einer neuen Generation.
* Legen Sie ein neues Feld an. Berechnen Sie den neuen Zustand
* aller Feldelement aus dem alten Feld
*/
void neueGeneration() {
// Tipps:
// Weisen Sie die aktuelle Generation auf die alte zu
// Erzeugen oder wiederverwenden Sie ein Feld für eine neue Generation
// Nutzen Sie eine doppelt geschachtelte Schleife zum Ueberstrichen des aktuellen Felds
// Zaehlen Sie die Nachbarn der aktuellen Position in der alten Generation
// Achten Sie auf die Feldgrenzen!!
// Setzen Sie den Wert des aktuellen Felds auf "true" falls ein Objekt erhalten oder erzeugt werden soll
// Setzen Sie dem Wert des aktuellen Felds auf "false" falls kein Objekt in der neuen Generation existieren soll
}
/**
* Das Feld mit den aktuellen Werten
* @return
*/
public boolean[][] status() {return null;} // Hier das aktuelle Feld zurückgeben
}
Klasse SpielDesLebens.java
Das Hauptprogramm. Achten Sie auf die Paketstruktur!
Beim vorgebenen Paket kann das Programm mit dem folgenden Befehl gestartet werden
$ java s1.block7.SpielDesLebens
package s1.block7;
import javax.swing.*;
import java.awt.*;
import java.awt.event.ActionEvent;
import java.awt.event.ActionListener;
import java.awt.image.BufferedImage;
/**
* Das Spiel des Lebens nach Conway
* @author s@scalingbits.com
*/
public class SpielDesLebens extends JApplet implements Runnable {
final private int size;
final private int xRaster=10;
final private int yRaster=10;
final private Generation gen;
final private JButton[][] buttonFeld;
private static boolean appletMode = true;
private static boolean autoMode = false;
private ImageIcon belegtIcon;
private ImageIcon freiIcon;
private static SpielDesLebens myself;
private int sleeptime = 2000; // Millisekunden im Automode
public class Zelle extends JButton {
final public int x;
final public int y;
public Zelle (Icon ic, int x, int y) {
super(ic);
this.x=x;
this.y=y;
}
}
/**
* Der Konstruktor ohne Argumente wird nur beim einem Start als Applet
* benutzt. Hier wird ein Applet mit einem Grid erzeugt.
*/
public SpielDesLebens() {
erzeugeIcons();
myself=this;
gen = new Generation();
size = gen.groesse();
JFrame f = null;
if (!appletMode) f = new JFrame("Game");
JPanel jp = new JPanel();
jp.setLayout(new GridLayout(size, size));
buttonFeld = new JButton[size][size];
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
buttonFeld[i][j] = createButton(i, j);
jp.add(buttonFeld[i][j]);
}
}
JButton naechste = new JButton(">");
naechste.setToolTipText("Erzeuge nächste Generation");
naechste.addActionListener(new ActionListener() {
@Override
public void actionPerformed(ActionEvent ae) { nextGen();}
} // Ende innere Klasse
);
JButton auto = new JButton(">>>");
auto.setToolTipText("Starte Film");
auto.addActionListener(new ActionListener() {
@Override
public void actionPerformed(ActionEvent ae) {
sleeptime /=2; // Verdoppeln der Geschwindigkeit
if (!autoMode) {
autoMode=true;
Thread t1 = new Thread(SpielDesLebens.myself);
t1.start();
}
}
} // Ende innere Klasse
);
JButton stop = new JButton("Stop");
stop.setToolTipText("Stoppe Film");
stop.addActionListener(new ActionListener() {
@Override
public void actionPerformed(ActionEvent ae) {
autoMode=false;
sleeptime=4000;
}
} // Ende innere Klasse
);
JPanel buttonPanel = new JPanel();
buttonPanel.add(naechste);
buttonPanel.add(auto);
buttonPanel.add(stop);
Container co;
if (!appletMode) co =f;
else co=this;
co.setLayout(new BorderLayout());
co.add(jp,BorderLayout.CENTER);
co.add(buttonPanel,BorderLayout.SOUTH);
co.setPreferredSize(new Dimension(size * (xRaster+3),size * (yRaster+3)));
if (!appletMode) {
f.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
f.pack();
f.setVisible(true);
}
}
/**
* Starten der Anwendung als eigenständiges Programm
* @param args werden nicht benutzt
*/
public static void main(String[] args) {
appletMode = false;
SpielDesLebens k = new SpielDesLebens();
}
/**
* Erzeugen eines JButtons für jede Zelle des Feldes
* @param xx x Koordinate im Feld
* @param yy y Koordinate im Feld
* @return einen Buttton mit ActionListener
*/
private JButton createButton(int xx, int yy) {
JButton myButton = new Zelle(freiIcon,xx,yy);
myButton.setToolTipText(("("+xx+","+yy+")"));
myButton.addActionListener(new ActionListener() {
@Override
public void actionPerformed(ActionEvent ae) {
if(!autoMode) {
Zelle f = (Zelle) ae.getSource();
//System.out.println("Action auf" +f.x + " " + f.y);
boolean[][] g = gen.status();
if (g[f.x][f.y]) {
f.setIcon(freiIcon);
g[f.x][f.y]=false;
}
else {
f.setIcon(belegtIcon);
g[f.x][f.y]=true;
}
f.updateUI();
}
}
} // Ende innere Klasse
);
return myButton;
}
/**
* Erzeuge die beiden Ikonen für eine freies und ein belegtes Feld
*/
public final void erzeugeIcons() {
BufferedImage belegt =
new BufferedImage(xRaster, yRaster, BufferedImage.TYPE_4BYTE_ABGR);
Graphics2D g = belegt.createGraphics();
g.setColor(Color.white);
g.fillRect(0, 0, xRaster-1, yRaster-1);
g.setColor(Color.black);
g.fillOval(1, 1, xRaster-2, yRaster-2);
g.dispose();
belegtIcon = new ImageIcon(belegt);
BufferedImage frei =
new BufferedImage(xRaster, yRaster, BufferedImage.TYPE_4BYTE_ABGR);
g = frei.createGraphics();
g.setColor(Color.white);
g.fillRect(0, 0, xRaster-1, yRaster-1);
g.dispose();
freiIcon = new ImageIcon(frei);
}
/**
* Erzeugen einer neuen Generation und Abgleich der JButtons mit neuen
* Ikonen
*/
private void nextGen() {
gen.neueGeneration();
boolean[][] stat = gen.status();
for (int i = 0; i < size; i++)
for (int j = 0; j < size; j++)
if (stat[i][j]) buttonFeld[i][j].setIcon(belegtIcon);
else buttonFeld[i][j].setIcon(freiIcon);
}
/**
* Lasse neue Generationen automatisiert in einem eigenen Thread
* erzeugen
*/
@Override
public void run() {
try {
while (autoMode) {
Thread.sleep(sleeptime);
nextGen();
}
} catch (InterruptedException e) {
System.out.println(e.getMessage());
}
}
}
Lösung der Aufgabe in Zwischenschritten
1. Die Anwendung übersetzt und läuft fehlerfrei
- Variable für Feldgröße als Objektvariable dekarieren und mit Konstante belegen
- Wert 5 wählen; Fenster per Hand vergrößern
- Methode zur Rückgabe der Feldgröße implementieren
- Zweidimensionales Feld als Objektvariable für aktuelles Feld deklarieren. Benutzen Sie den Typ boolean.
- Im Konstruktor alle Zellen des Felds mit doppelt geschachtelter Schleife initialisieren
- Methode zur Rückhabe des Felds implementieren
- Methode neueGeneration() implementieren:
- Trivialimplementierung die genau ein beliebiges aber festes Feldelement auf "true" setzt
- Testen der Implementierung: Initialiserung des aktuellen Feldes kann so getestet werden
Ergebnis
Es wurde als Feldgröße 20 verwendet. Es wurde die Zelle [3,3] auf true gesetzt
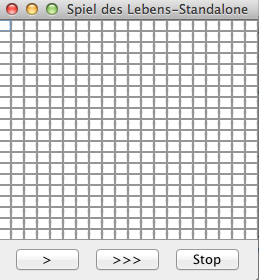
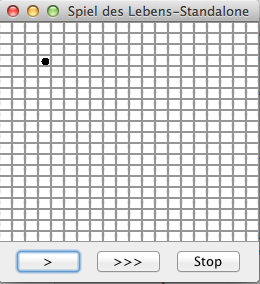
| 1. Nach Starten des Programms | 2. Nach Klicken des ">" Button | 3. Nach mehrfachem Kicken auf Zellen |
|---|---|---|
 |
 |
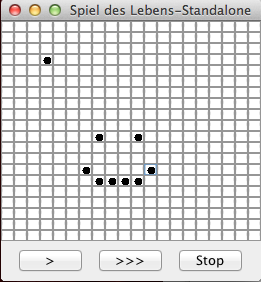 |
Der Benutzer sollte in der Lage sein, den Zustand von Zellen durch einfaches anklicken zu invertieren. Hier wurde im Schritt 3 ein "Happy Face" gezeichnet.
Die Position [3,3] sollte man jetzt auch mit einem Mausklick löschen können. Nach Klicken des ">" Button sollte das Pixel wieder gezeigt werden weil die Methode neueGeneration() aufgerufen wurde.
2. Zellen abhängig von anderen Zellen belegen: Methode neueGeneration()
Erweitern Sie die Methode neueGeneration()
- Setzen Sie jedes Feldelement (x,y) auf "true" wenn das Element (x+1.y+1) belegt ("true") war. Hierdurch werden aus Punkten Striche die sich nach rechts unten fortpflanzen.
- Sie benötigen hierfür eine doppelt geschachtelte Schleife die alle Feldelemente abarbeitet.
- Achten Sie darauf, dass Sie keine Elemente auf Positionen die größer als die Feldgrenze sind!
- Testen Sie die Anwendung: Jeder Punkt sollte in der Nachfolgegeneration einen neuen links oberhalb erhalten. Es steht pro Generation eine neue belegte Zelle links oberhalb.
Ergebnis
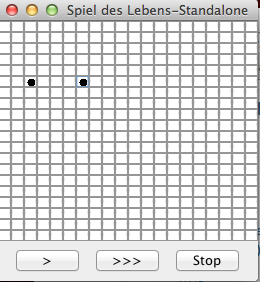
Es wurde als Feldgröße 20 verwendet. Es wurden Zellen nach dem Start des Programms mit der Maus markiert:
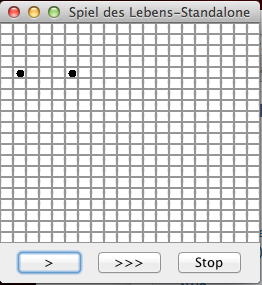
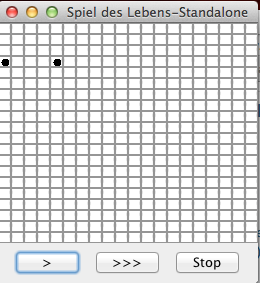
| 1. Nach Starten des Programms und Markieren zweier Zellen | 2. Nach Klicken des ">" Button | 3. Nach zweitem Klicken des ">" Buttons |
|---|---|---|
 |
 |
 |
3. Berechnen einer neuen Generation aus einer alten Generation
Man benötigt zu Lösung der Aufgabe zwei Felder. Das erste Feld enthält die Zellen der alten Generation. Das zweite Feld wird für die Belegung der neuen Generation benötigt. Mit nur einem Feld würde man nicht zwischen alter und neuer Generation entscheiden können. Man würde Zellen inkorrekt berechnen und belegen.
- Deklarieren Sie eine weitere Objektvariable die auf das alte Feld zeigt
- Initialisieren Sie das Feld in der gleichen Größe im Konstruktor. Belegen Sie alle Zellen mit dem Wert "false";
- Erweitern Sie die Methode neueGeneration()
- Referenzieren Sie mit dem Zeiger der alten Generation die aktuelle Generation.
- Erzeugen sie ein Feld für die neue (aktuelle) Generation
- Initialiseren Sie das neue Feld mit vernünftigen Werten.
- Belegen Sie jedes Feld der neuen Generation mit "true" wenn der rechte, untere Nachbar der Vorgängergeneration existiert. Dieses Problem wurde schon in der vorgehenden Phase gelöst.
- Testen Sie die Anwendung: Sie soll die gleichen Ausgaben produzieren
- Setzen Sie die Größe des Felds wieder auf 50 (oder mehr)
Jetzt sollte das Umkopieren von neuen auf alte Generationen funktionieren. Alle Schleifen sollten fehlerfrei laufen.
4. Berechnen der korrekten Nachbarschaftsbeziehung in der Methode neueGeneration()
Erweitern Sie die Methode neueGeneration()
- Zählen Sie für jedes Feld die Anzahl der Nachbarn. Achten Sie auf die Feldgrenzen. Prüfen Sie keine Feldelemente ab, die ausserhalb des Feldes liegen.
- Bestimmen Sie anhand der Nachbarn und es dem Wert der alten Zelle den Zustand der aktuellen Zelle.
Ergebnis
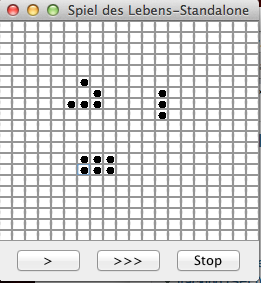
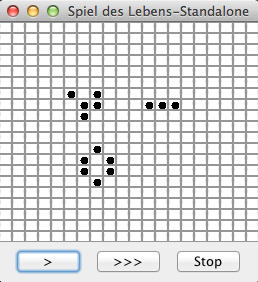
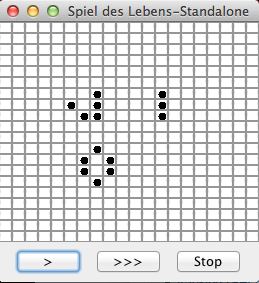
Es wurde als Feldgröße 20 verwendet. Nach dem Start wurde mit der Maus ein "Glider", ein senkrechter Dreierbalken und ein Rechteck aus sechs Zellen gezeichnet.
| 1. Nach Starten des Programms und Markieren diverser Zellen | 2. Nach Klicken des ">" Button | 3. Nach zweitem Klicken des ">" Buttons |
|---|---|---|
 |
 |
 |
7.4.5 Flughafenbeispiel mit Feldern
Klasse Flughafen
package airline.block7;
/**
*
* @author stsch
*/
public class Flughafen {
String name;
Flugzeug[] gate;
double treibstoffLager;
public Flughafen(int anzahlGates) {
gate = new Flugzeug[anzahlGates];
}
public void drucken() {
System.out.println("*** Unser Flughafen ***");
System.out.println("Flughafen " + name);
for (int i =0;i<gate.length;i++)
System.out.println("Am Gate " + i + ": " + gate[i]);
System.out.println("Treibstoff: " + treibstoffLager);
System.out.println("***********************");
}
public static void main(String[] args) {
Flughafen pad = new Flughafen(6);
pad.name="Paderborn";
pad.treibstoffLager = 1000000;
pad.drucken();
// Boeing 747, https://de.wikipedia.org/wiki/Boeing_747#747-400
Flugzeug lh1 = new Flugzeug(40000, 400000);
lh1.kennzeichen ="D-ABTL";
lh1.einsteigen(3);
System.out.println("Unsere grosse Gesellschaft" + Flugzeug.meineLG());
double aktuellesGewicht = lh1.gewicht();
System.out.println("aktuelle Gewicht von lh1: " + aktuellesGewicht);
pad.gate[1] = lh1;
// Airbus A380 https://de.wikipedia.org/wiki/Airbus_A380#A380-800
Flugzeug lh2 = new Flugzeug(40000, 400000, "D-AIMA");
lh2.einsteigen(11);
lh2.einsteigen();
lh2.einsteigen(4);
// Wir wollen wieder austteigen
lh2.aussteigen(5);
pad.gate[2] = lh2;
System.out.println("Flughafen " + pad.name);
System.out.println("Am Gate 1: " + pad.gate[1].kennzeichen +
" Passagiere: " + pad.gate[1].getPassagiere() +
" akt. Gewicht: " + pad.gate[1].gewicht());
System.out.println("Am Gate 2: " + pad.gate[2].kennzeichen +
" Passagiere: " + pad.gate[2].getPassagiere() +
" akt. Gewicht: " + pad.gate[2].gewicht());
pad.drucken();
}
}
Klasse Flugzeug
package s1.airline.block7;
/**
* Das ist ein Flugzeug des 7.ten Blocks
* @author s@scalingbits.com
*/
public class Flugzeug {
final static double durchschnittsgewicht = 75;
String kennzeichen;
private int passagiere;
int maxPassagiere = 100;
final double maximalesGewicht;
final double leerGewicht;
public int getPassagiere() {
return passagiere;
}
public Flugzeug(double minGewicht, double maxGewicht) {
System.out.println("Ich baue jetzt ein Flugzeug");
if (minGewicht > 0) leerGewicht = minGewicht;
else leerGewicht = 0;
if ((maxGewicht > 0) && (maxGewicht>=leerGewicht))
maximalesGewicht = maxGewicht;
else maximalesGewicht = leerGewicht;
passagiere = 0;
}
public Flugzeug(double minGewicht, double maxGewicht, String kennz) {
this(minGewicht,maxGewicht);
kennzeichen = kennz;
}
/**
* Einsteigen eines einzelnen Passagiers
*/
public void einsteigen() {
if (passagiere >= maxPassagiere) { // Zuviele Einsteiger
System.out.println("Fehler: Einsteigen verweigert ");
} else { // passt schon
passagiere++;
}
}
/**
* Einsteigen einer vorgegebenen Anzahl Passagiere.
* und sie funktioniert auch!
* Wenn zuviele einsteigen möchten, darf keiner einsteigen!
* @param einsteiger Anzahl der Passagiere die einsteigen.
*/
public void einsteigen(int einsteiger) {
if (passagiere+einsteiger > maxPassagiere) {
System.out.println("Fehler: Einsteigen verweigert ");
} else {
System.out.println("Ich lasse " + einsteiger + " Passagiere eingestiegen");
einsteigen(); // Einer steigt ein
if (einsteiger > 1)
einsteigen(einsteiger-1); //Der Rest steigt ein
}
}
public void aussteigen(final int aussteiger) {
if (passagiere >= aussteiger) {
passagiere -= aussteiger;
} else {
System.out.println("Fehler: Flugzeug ist leer... ");
}
} // Ende der Methode aussteigen
/**
* berechnet das aktuelle Gewicht des Flugzeugs
* @return aktuelle Gewicht
*/
public double gewicht() {
//double g = leerGewicht+passagiere*durchschnittsgewicht;
return leerGewicht+passagiere*durchschnittsgewicht;
}
public static String meineLG() { return "Lufthansa";}
}
- Printer-friendly version
- Log in to post comments
- 8662 views
